Метод Зейделя (модификация метода итераций).

При решении системы линейных алгебраических уравнений вида (1) методом итераций значение вычисляется по значениям с предыдущей итерации , , ... , 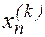путем подстановки в правую часть системы (4).

Можно ожидать, что приближения будут быстрее сходиться к решению системы, если сразу же после вычисления , при вычислении последующих использовать , а не в правой части (4).

Процедура вычисления через , ,..., , , называется методом Зейделя и записывается в развернутой форме в виде:

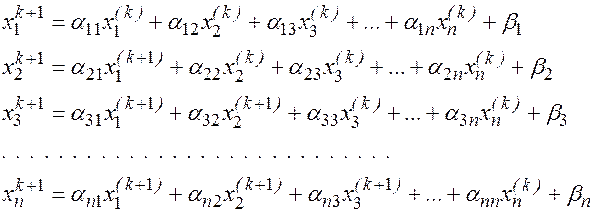(9)

Запишем метод Зейделя в векторной форме, для этого представим матрицу a в виде суммы двух треугольных матриц L и U, где

,

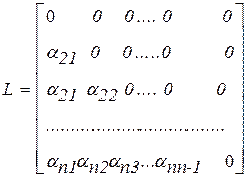Тогда систему (9) можно записать в виде матричного равенства:

(10)

Матрица (E-L) - неособенная, т.е. имеет обратную (E-L)^-1, следовательно, можно выразить х^(k+1) из (10)

Из (10) получаем, что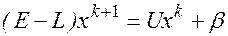

Обозначим

тогда

(11)

Следовательно, метод Зейделя для системы (1) эквивалентен методу простой итерации x = ax + b для системы x = Px + Q, где матрица P и вектор Q определены выше.

Теперь для сходимости (11) достаточно, чтобы ||P||₁ < 1 или ||P||₂ < 1.

х = aх + b (2)

выполнено условие , где , то процесс (9) для системы (2) сходится к единственному решению при любом выборе начального приближения.

Доказательство: ………………………………………………………………………………

Оценим погрешности приближений по методу Зейделя.

Пусть и - две последовательные итерации процесса Зейделя.

Применяя к этим итерациям преобразования, получим:

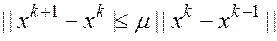
Выполним аналогичные (как для МПИ) преобразования для разности между (k+m)- м и k -м членами последовательных приближений по Зейделю при некотором mÎN :

Рассматривая итоговое равенство при , переходя к пределу получим утверждения теоремы:

, где

Тогда условие окончания итерационного процесса Зейделя будет иметь вид:

или

Тогда или

,