Расчетные формулы. Основным ограничением метода является предположение о том, что все элементы

ПРЯМОЙ ХОД:

(7)

ОБРАТНЫЙ ХОД:

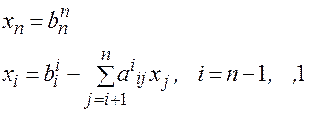(8)

Основным ограничением метода является предположение о том, что все элементы , на которые проводится деление, отличны от нуля. Число называется ведущим элементом на к – том шаге исключения.

Полезно после определения x_i вычислить невязки

Невязка – это количественная мера несоответствия между правыми и левыми частями уравнений системы при подстановке в них вычисленного решения.

Так как реальные машинные вычисления производятся не с точными, а с усеченными числами, т.е. неизбежны ошибки округления, то анализируя, например, формулы прямого хода, можно сделать вывод о том, что выполнение алгоритма может прекратиться или привести к неверным результатам, если знаменатели дробей на каком – то этапе окажутся равными нулю или очень маленькими числами.

Чтобы уменьшить влияние ошибок округления и исключить деление на нуль, на каждом этапе прямого хода уравнения системы обычно переставляются так, чтобы деление производилось на наибольший по модулю в данном столбце элемент. Числа, на которые производится деление в методе Гаусса, называются ведущими или главными элементами. Отсюда название модификации метода, исключающей деление на нуль и уменьшающей вычислительные погрешности, метод Гаусса с выбором главного элемента (оптимальный метод Гаусса).