С) c - норма (равномерная или Чебышевская норма вектора x)

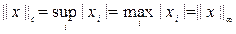
В 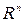имеют место соотношения:

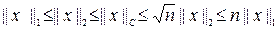
т.е. в 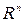все эти нормы эквивалентны и сходимость в любой из них влечет сходимость в остальных нормах.

Проверим, например:

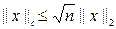
Имеем:

2). Норма матрицы А. Норма матрицы А, согласованная с нормой вектора x определяется следующим образом:

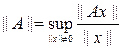
Отсюда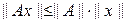

Это условие согласования норм ||x|| и ||A||.

Можно проверить, что введенная таким образом норма матрицы удовлетворяет неравенствам:

,

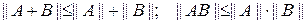Для квадратных матриц наиболее употребительны следующие нормы:

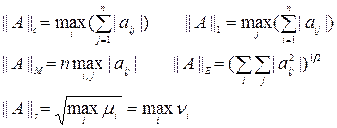
(где 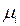- собственные значения симметричной самосопряженной матрицы , ).

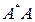Первые две нормы не имеют специальных названий:

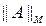- называется максимальной,

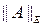- сферической или евклидовой,

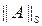- спектральной.

Умножая вектор х на матрицу А, получаем новый вектор Ах, норма которого может сильно отличаться от нормы вектора х.

Величину можно рассматривать как своеобразный «коэффициент растяжения» вектора х матрицей А. Для некоторых векторов он может быть малым, а для некоторых большим.

Если M и m – максимальное и минимальное значение коэффициента растяжения, то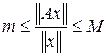

Нормой матрицы А называется максимальное значение коэффициента растяжения:

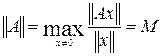
Минимальное значение коэффициента растяжения также играет важную роль в линейной алгебре.

Если А – невырожденная матрица, то для нормы обратной матрицы справедливо равенство:

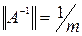
Обусловленность матрицы. Погрешности.

Вернемся к анализу формулы (4) для вариации решения x

1. 1. Пусть матрица А известна точно ( ) и погрешность решения связана лишь с погрешностью 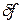правой части, тогда:

Из:

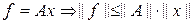
Перемножая полученные неравенства, найдем:

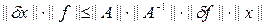
Или

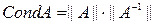=M/m - число обусловленности матрицы А.

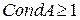- всегда (в любой норме), т.о. хорошо обусловленные матрицы – это матрицы с малым 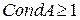, при этом относительная погрешность решения мала.

2. 2. Пусть известно возмущение матрицы А, при условии, что правая часть f задана точно.

Тогда:

Или

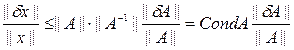
Таким образом, чем больше число обусловленности, тем чувствительнее система к округлениям.

Системы с большим числом обусловленности называют плохо обусловленными.

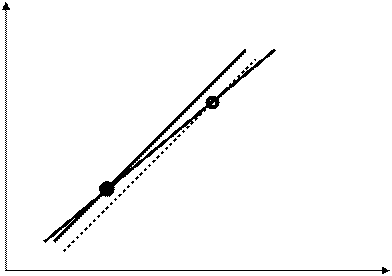
В случае СЛАУ 2-го порядка понятие обусловленности матрицы допускает наглядную геометрическую интерпретацию.

ЛЕКЦИЯ №2

Метод последовательного исключения
неизвестных – метод Гаусса.

Методы решения систем линейных алгебраических уравнений (СЛАУ):
1) точные (прямые)
2)приближенные ( методы последовательных приближений.)

Прямые методы : метод Крамера, метод Гаусса и его модификации: (метод главного элемента, метод квадратного корня, метод отражений и другие), метод ортогонализации. N £ 10³.

Методы последовательных приближений (итерационные):

метод простой итерации,

метод Зейделя,

метод релаксаций,

градиентные методы и их модификации. N¸ 10⁶.

Рассмотрим систему n линейных алгебраических уравнений с n неизвестными:

(1)

в матричном виде: Ax = b;

здесь 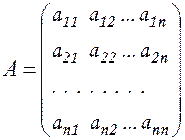- квадратная матрица размера n´n,

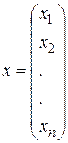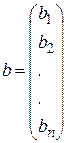, - векторы n-го порядка.

В индексной форме:

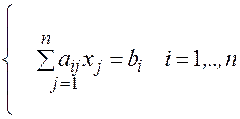(2)

Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной (противоречивой), если она не имеет решений.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если более одного решения.