КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Степени вершин графа
В этом пункте граф будет предполагаться неориентированным.
Степенью вершины графа называется количество ребер, инцидентных вершине. Необходимо, однако, уточнить понятие степени в случае, когда среди ребер, инцидентных данной вершине, есть петля. Можно считать петлю за одно ребро, а можно — за два (подразумевая, что петля имеет «два входа» в вершину). В первом случае степень вершины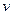 
будет обозначаться 
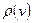, во втором — 
.
Пример.
Для вершины 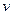данного графа 
, 
.
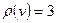Теорема.
Пусть граф имеет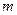 
ребер и 
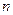вершин 
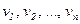. Тогда
.
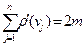Доказательство: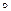 
В самом деле, каждое ребро, не являющееся петлей, инцидентно двум вершинам, следовательно, входит в данную сумму два раза; петли также дважды учитываются в этой сумме. 
Следствие.
Число вершин графа нечетной степени 
четно.
Уже эта простая теорема позволяет решить ряд интересных задач.
Пример. Утверждают, что в одной компании из 7 человек каждый знаком с тремя и только тремя другими. Возможна ли такая компания?
Построим граф знакомств для этой компании, сопоставив каждому из 7 человек вершину, которая соединяется ребрами со знакомыми ему людьми (вершинами). Степень каждой из 7 вершин равна 3. Согласно теореме этого быть не может.
Дата добавления: 2014-12-03; просмотров: 196; Мы поможем в написании вашей работы!; Нарушение авторских прав |