КИНЕМАТИКА ТОЧКИ

Для задания движения точки применяется один из следующих способов: векторный, координатный или естественный.

Векторный способ. Рассмотрим движение точки М относительно заданного неподвижного центра О. Положение точки М в произвольный момент времени t можно определить, задав ее радиус-вектор , проведенный из центра О в точку М, как вектор-функцию времени:

. (1.1)

Уравнение (1.1) называется уравнением движения точки в векторной форме. При движении точки М конец радиус-вектора описывает кривую, называе-мую траекторией точки.

Скоростью точки М в момент времени t называется вектор равный производной от радиус-вектора по времени:

. (1.2)

Рис. 1.1

Вектор скорости характеризует изменение радиус-вектора точки в единицу времени по модулю и направлению. Вектор скорости направлен так же, как вектор элементарного перемещения 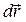по каса-тельной к траектории в данной точке М (рис. 1.1). Размерность скорости , где L - длина, Т - время. Единицами измерения скорости могут быть м/c, cм/c, км/ч.

Ускорением точки М в момент времени t называется вектор , равный производной от вектора скорости точки, по времени:

. (1.3)

Вектор ускорения характеризует изменение вектора скорости точки в единицу времени по модулю и направлению. Вектор ускорения направлен в точке М в сторону вогнутости траектории (рис. 1.1). Размерность ускорения , поэтому оно измеряется в м/с² или см/с².

Если угол между векторами и острый, то движение точки ускоренное, а если угол тупой, то - замедленное. Если угол между векторами и равен 90°, то точка равномерно движется по траектории.

Координатный способ. С точкой О свяжем неподвижную ортогональную декартовую систему координат ОXYZ и зададим координаты точки М(x, y, z) как функции времени:

. (1.4)

Уравнения (1.3) называются уравне-ниями движения точки в декартовых координатах. Уравнение траектории точки можно определить исключением времени t как параметра из уравнений (1.3).

Учитывая связь

,

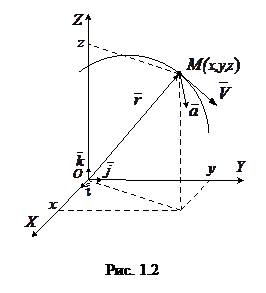
( - единичные орты декартовых осей OX, OY, OZ на рис. 1.2), определения (1.2) и (1.3), найдем скорость и ускорение точки в декартовых координатах:

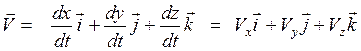, (1.5)

. (1.6)

Из (1.5) и (1.6) следует, что

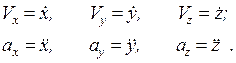(1.7)

Проекции вектора скорости точки на декартовые оси равны первым производным, а проекции вектора ускорения - вторым производным от соответствующих координат по времени. В (1.7) и далее производная по времени обозначается точкой, стоящей над величиной .

Скорость и ускорение точки по величине определяется по формулам:

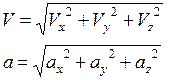(1.8)

Направление векторов и найдем с помощью косинусов направляющих углов с осями OX, OY, OZ:

(1.9)

Естественный способ. Для задания движения точки естественным способом необходимо:

1) знать траекторию движения точки;

2) выбрать на траектории начало отсчета «О»;

3) установить положительное и отрицательное направление отсчета криволинейной координаты ОМ;

4) задать закон изменения криволинейной координаты s как функции времени: .

Свяжем с точкой М естественный трехгранник, образованный единичными векторами , составляющими пра-вую тройку ( 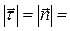(рис. 1.3); век-тор направим в точке М по касательной к траектории в сторону положительного отсчета ОМ; вектор 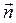- по главной нормали к центру кривизны траектории; вектор - по бинормали к траектории.

Радиус вектор точки М относительно начала декартовой системы координат будет сложной функцией времени: 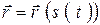. Поскольку , то из дифференциальной геометрии известно, что ]

, (1.10)

где - радиус кривизны траектории в точке М. Используя (1.2), (1.10) и правило вычисления производной от сложной функции, получаем

или

, (1.11)

где числовое значение скорости

. (1.12)

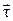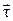Числовое значение скорости точки равно первой производной от криволинейной координаты s по времени. Из (1.11) следует, что вектор скорости точки направлен по касательной к траектории вдоль орта (в сторону положительного отсчета s), если (рис. 1.4), и против орта , если .

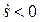Дифференцируя (1.11) по времени, найдем ускорение точки при естественном способе задания движения:

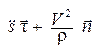
или

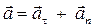. (1.13)

Здесь

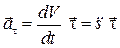(1.14)

вектор касательного ускорения точки, его числовое значение , а

(1.15)

вектор нормального ускорения точки, его числовое значение .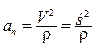

Формула (1.13) выражает теорему Гюйгенса: ускорение точки при криволинейном движении равно геометрической сумме касательного и нормального ускорений. Из (1.13) следует, что проекция ускорения точки на бинормаль всегда равна нулю: .

Вектор касательного ускоре-ния 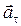направлен в точке М по касательной к траектории в соот-ветствии со знаком (аналогич-но вектору скорости ). Вектор нормального ускорения на-правлен вдоль главной нормали к центру кривизны траектории (рис. 1.4).

Поскольку векторы 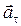и взаимно перпендикулярны, то вектор ускоре-ния точки М изобразим диагональю прямоугольника, построенного на составляющих 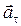и как на сторонах. Его модуль и направление определяются по формулам

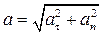; (1.16)

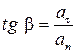. (1.17)

Если знаки и в данный момент времени одинаковые (оба положительные (рис. 1.4) или отрицательные), то точка движется ускоренно, а если знаки противоположные - замедленно.

Рассмотрим некоторые частные случаи движения точки.

Прямолинейное движение точки. Так как траекторией точки является прямая линия, то . Тогда и . Касательное ускорение характеризует изменение скорости по величине.

Равномерное криволинейное движение точки. При этом движении величина скорости точки остается постоянной , поэтому , и , т. е. вектор ускорения точки 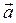направлен по главной нормали. Нормальное ускорение точки характеризует изменение ее скорости по направлению.

Определим закон равномерного криволинейного движения точки, если при . Так как 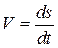, то , тогда

,

. (1.18)

Формула (1.18) определяет закон равномерного движения точки.

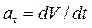Равнопеременное криволинейное движение точки. При этом движении . Определим скорость точки и закон ее движения по известной кривой. Пусть при . Поскольку , то ;

.

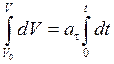Следовательно,

или

, (1.19)

где знак «+» соответствует равноускоренному движению, а знак «-» - равно-замедленному движению точки.

С учетом (1.12), выражение (1.19) запишем в виде

.

Отсюда

,

. (1.20)

Формула (1.20) определяет закон равнопеременного криволинейного движения точки.

Равномерное прямолинейное движение точки. В этом случае вектор скорости не изменяется ни по величине, ни по направлению: 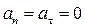и . Таким образом, единственным движением, при котором ускорение точки равно нулю, является равномерное прямолинейное движение.

Определим касательное и нормальное ускорения точки и значение радиуса кривизны ее траектории, если движение точки задано в координат-ной форме (1.3):

.

Из (1.8) имеем . Вычислим производную по времени от данного равенства:

,

отсюда

. (1.21)

Из (1.16) находим нормальное ускорение точки

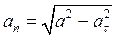. (1.22)

Тогда значение радиуса кривизны траектории в точке М определим по формуле

(1.23)