ВРАЩАЮЩЕГОСЯ ТЕЛА

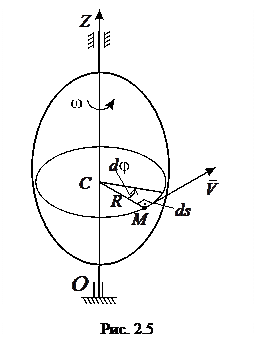Пусть тело вращается вокруг оси OZ и имеет в данный момент времени угловую скорость и угловое ускорение ( 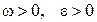). Рассмотрим произвольную точку М тела. При вращении тела вокруг оси траекторией точки М является окружность радиусом R, лежащая в перпендикулярной к оси плоскости (рис. 2.5). Вектор скорости 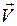точки М будет направлен по касательной к этой окружности ( 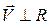) в направлении вращения тела, а его величина определяется по формуле (1.12)

.

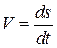Выразим элементарное перемещение 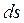точки М через элементарный угол поворота 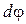тела. Запишем пропорцию

.

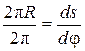Отсюда 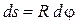. Тогда

,

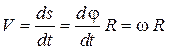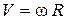. (2.12)

Для определения ускорения точки М воспользуемся теоремой Гюйгенса (1.13)

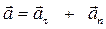. (2.13)

Найдем выражения для касательного и нормального ускорений точки через угловую скорость и угловое ускорение тела:

,

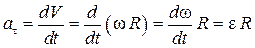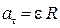; (2.14)

,

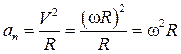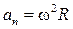. (2.15)

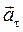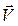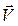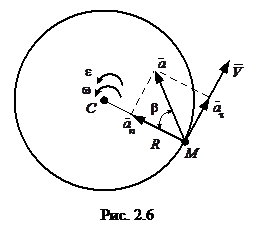
Касательное ускорение направлено по касательной к траектории в точке М (по вектору при ускоренном вращении и против вектора при замедленном вращении). Вектор нормального ускорения 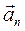всегда направлен по радиусу вращения МС = R к оси вращения тела (рис. 2.6).

Величина полного ускорения точки вращающегося тела вычисляется по формуле

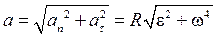(2.16)

Отклонение вектора полного ускорения 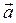от радиуса R описываемого точкой М окружности определяется углом :

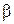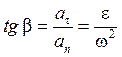. (2.17)

Поскольку точка М выбрана произ-вольно, то из (2.16) и (2.17) следует, что ускорения всех точек вращающегося твердого тела пропорциональны их расстояниям до оси вращения и в данный момент времени образуют одинаковые углы 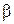с радиусами описы-ваемых ими окружностей.

ВЫРАЖЕНИЯ СКОРОСТИ ТОЧКИ,