Рассмотрим вектор . Вычислив модуль этого вектора

Рис. 2.7

,

заметим, что он равен численному значению скорости точки М. Направления векторов 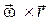и также совпадают (оба вектора направлены перпендикулярно плоскости треугольника ОМС, т. е. по касательной к окружности в направлении вращения тела). Следовательно,

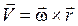. (2.18)

Вектор скорости точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор точки. Формула (2.18) называется формулой Эйлера.

Согласно (1.2), , и при вращательном движении тела радиус-вектор 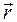точки, изменяя своё направление, остаётся постоянным по модулю 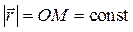. Тогда из (2.18) получим выражение для полной производной по времени от вектора 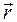изменяющегося по направлению с угловой скоростью w, но постоянного по модулю:

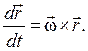(2.19)

Для определения ускорения точки М продифференцируем по времени равенство (2.18):

.

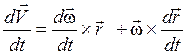Отсюда находим выражение полного ускорения точки вращающегося тела

, (2.20)

где касательное и нормальное ускорения соответственно равны

(2.21)

Действительно, модули этих векторов одинаковы:

;

.

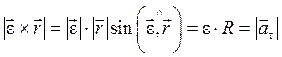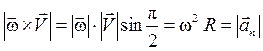Вектор 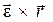направлен так же, как вектор 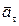, по касательной к траектории точки М, а вектор 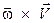так же, как вектор нормального ускорения 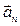, по радиусу МС к оси вращения (см. рис 2.7).