Диференціальне рівняння вільних затухаючих коливань і його розв’язування

Розглянемо вільні затухаючі коливання, амплітуда яких внаслідок втрат енергії реальною коливальною системою зменшується з часом. Найпростішим механізмом зменшення енергії коливань є її перетворення в теплоту внаслідок тертя в механічних коливальних системах, а також омічних втрат і випромінювання електромагнетної енергії в електричних коливальних системах.

Закон затухання коливань визначається властивостями коливальних систем. Як правило розглядають лінійні системи – ідеалізовані реальні системи, у яких параметри, які визначають фізичні властивості системи, у ході процесу не змінюються. Лінійними системами є, наприклад, пружинний маятник при малих деформаціях пружини (в межах дії закону Гука), коливальний контур, індуктивність, ємність і опір якого не залежать ні від струму в контурі, ні від напруги. Різні за своєю природою лінійні системи описуються ідентичними лінійними диференціальними рівняннями, які дозволяє підходити до вивчення коливань різної фізичної природи з єдиної точки зору.

Диференціальне рівняння вільних затухаючих коливань лінійної системи задається у вигляді

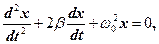(29)

де x – коливна величина, яка описує той або інший фізичний процес, – коефіцієнт затухання, ω₀ – циклічна частота вільних незатухаючих коливань тієї ж коливальної системи, тобто при (при відсутності втрат енергії).

Щоб знайти розв’язок рівняння (29), слід фізичну величину х виразити через нову змінну z відповідно до рівняння

(30)

де z = z (t). Після підстановки першої і другої похідних від рівності (30) в рівняння (29) одержимо

(31)

Розв’язок рівняння (31) залежить від знака коефіцієнта перед шуканою величиною. Розглянемо випадок, коли цей коефіцієнт позитивний, тобто .

Тоді одержимо рівняння типу

(32)

де

. (33)

Розв’язком рівняння (32) є рівняння типу (9) першої теми:

(34)

Після підстановки (34) у (30) для випадку малих затухань одержуємо розв’язок рівняння (29) у такому вигляді:

(35)

де 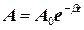─ амплітуда затухаючих коливань, А_о - початкова амплітуда.

Залежність (35) показана на рис. 11 суцільною лінією, а амплітуда коливань — пунктирними лініями.

Проміжок часу , протягом якого амплітуда затухаючих коли- вань зменшується у е разів, називається часом релаксації.

Затухання порушує періодичність коливань, тому затухаючі коливання не є періодичними, а тому до них поняття періоду або частоти незастосовне.

Однак якщо затухання мале, то можна умовно користуватися поняттям періоду як проміжку часу між двома наступними максимумами (або мінімумами) коливної фізичної величини (рис. 11).

Період затухаючих коливань з урахуванням формули (33) дорівнює

(36)

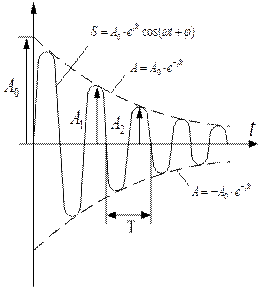
Рис. 11

Якщо Α (t) і Α (t + T) – амплітуди двох послідовних коливань, які відповідають моментам часу, що відрізняються на один період, то їх відношення

,

називається декрементом затухання,а його логарифм

(37)

називається логарифмічним декрементом затухання; N — число коливань,

які виконує коливна система за час зменшення амплітуди в е разів.

Для характеристики втрат енергії коливальною системою з часом, користуються поняттям добротності ,яка при малих значеннях логарифмічного декремента є помноженому на 2 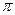відношенню повної накопленої системою енергії до середніх втрат енергії цією системою за час в один період, тобто

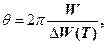(38)

де W ─ повна енергія системи; ΔW(T) ─ середні втрати енергії системою за час в один період (t=T).

Повна енергія коливної системи в момент часу t дорівнює

(39)

Енергія коливної системи через час в один період

(40)

Втрати енергії системою за час в один період дорівнюють

(41)

Добротність коливної системи одержимо, поділивши (39) на (41) і помноживши одержану величину на 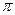2

(42)

У виразі (42) враховано, що відношення

У випадку, коли , то в формулі (42) період коливань T приймають рівним T₀.