
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Наближені обчислення зі значеннями тригонометричних функцій
Кількість значущих цифр в значені тригонометричних функцій кута залежить від того, з якою точністю заданий кут. В процесі вимірювання кута його значення може бути отримане з точністю до градуса або хвилини, секунди або іще точніше . Однак в шкільному курсі фізики значення кута зазвичай задано з точністю до градуса. Тому при розв’язуванні задач, в яких застосовуються тригонометричні функції, можна користуватись наступним правилам підрахунку цифр.
Правило 8. Якщо значення кута задано з точністю до градуса, то в значенні тригонометричної функції слід зберігати дві значущі цифри.
Наприклад:  ,
,  ,
,  ,
,  ,
,  .
.
Розглянемо приклад застосування правила 8 у фізичних задачах.
Задача 1.
Обчисліть роботу сили 1 Н (точно) на шляху 24,98 м, якщо кут між напрямком сили і напрямком переміщення рівний 550.
Розв’язування.

За умовою F=1 Н (точно), в числі s=24,98 м чотири значущі цифри, а за правилом 8, застосовуючи запасну цифру, можна записати:  . Тоді A=1.24,98.0,574.
. Тоді A=1.24,98.0,574.
Так, як число 0,574 має тільки дві значущі цифри, можна для спрощення обчислень попередньо заокруглити число 24,98 до трьох значущих цифр:  Дж.
Дж.
В фізичних задачах буває необхідно знайти значення кута за відомим значенням тригонометричної функції. Найбільш точно значення кута визначається за тангенсом або котангенсом.
Сформулюємо правило підрахунку цифр, що дозволяє знаходити значення кута з точністю до градуса. В більшості випадків це правило виявляється достатнім для розв’язування задач з шкільного курсу фізики.
Правило 9. Якщо значення тригонометричної функції має не менше двох правильних значущих цифр, то значення відповідного кута записують з точністю до градуса.
Приклади.
| sinα=0,12 | α 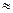 70 70
|
| cosβ=0,084 | β 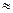 850 850
|
| tgγ=1,8 | γ 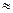 610 610
|
| tgφ=0,716 | φ 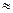 360 360
|
Розглянемо задачу, в якій застосовуються правила 8 і 9.
Задача 2.
Знайдіть кут заломлення сонячних променів, які падають на поверхню води під кутом 650 до горизонту.
Розв’язування.
Значення показника заломлення береться з трьома значущими цифрами (правило 6): n=1,33. Тому:
 .
.
В значенні sin 250 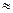 0,423 остання цифра запасна. Результат
0,423 остання цифра запасна. Результат 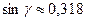 є проміжним тому запасну цифру поки що зберігаємо. Так, як
є проміжним тому запасну цифру поки що зберігаємо. Так, як  має дві значущі цифри, то у відповідності з правилом 9 значення кута беремо з таблиці з точністю до градуса:
має дві значущі цифри, то у відповідності з правилом 9 значення кута беремо з таблиці з точністю до градуса:  .
.
Правило 8 застосовується в тому випадку, коли значення кута задано з точністю до градуса. У випадку більшої точності задання кута потрібно мати на увазі таке доповнення до правила 8:
Доповнення. В тих випадках, коли значення кута задано з точністю до десятків хвилин, в значенні тригонометричної функції потрібно зберігати на одну або дві значущі цифри більше ніж рекомендується правилом 8.
Приклад.
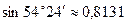 ,
,  ,
,  ,
,  .
.
При обчисленні із значеннями тригонометричних функцій можна користуватись і методом меж. Застосування цього методу ґрунтується на, тому, що за межами зміни значення кута легко знайти нижню і верхню межі значень кожної тригонометричної функції.
Дата добавления: 2014-12-03; просмотров: 406; Мы поможем в написании вашей работы!; Нарушение авторских прав |