Правило запасної цифри

Правило 5. При обчисленні проміжних результатів слід брати на одну цифру більше, ніж рекомендують попередні правила (1 – 4).

Якщо всяке заокруглення погіршує картину розподілу похибок в результаті якої – небудь дії, то збереження (згідно правила 5) однієї зайвої цифри в результатах проміжних обчислень і буде тим розумним компромісом в обчисленнях. В кінцевому результаті ця зайва цифра повинна бути відкинута, так як її збереження здійснювало би ілюзію підвищення точності.

Розглянемо приклад використання правила запасної цифри.

Задача 1.

Вагонетка скочується похилою гіркою з початковою швидкістю 2,6 м/с і прискоренням 0,65 м/с². Обчислити шлях пройдений вагонеткою за 4,8 с?

Розв’язування.

,

.

Перша проміжна дія: 2,6^.4,8=12,48 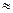12,5 м.

В результаті ми зберегли запасну цифру.

Дещо складніше обчислюється другий доданок: 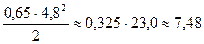м.

В цьому випадку правило запасної цифри застосовано три рази: при діленні на 2, при піднесенні до квадрата і при множенні. Отже, S=12,5+7,48=19,98 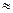20 м.

При обчисленні суми застосовано правило 1. Так, як цифра десятих в першому доданку запасна, то кінцевий результат був заокруглений до цілих.