
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод меж
При цьому методі кожне обчислення, пов’язане з розв’язком задачі, необхідно проводити двічі: перший раз для знаходження числа, меншого від шуканого точного результату – нижньої межі (НМ), другий раз – числа, більшого за шукане – верхньої межі (ВМ). В кінцевому результаті беруть півсуму меж:  . При цьому межа абсолютної похибки рівна піврізниці меж:
. При цьому межа абсолютної похибки рівна піврізниці меж: 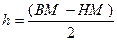 .
.
Наведемо правила обчислень НМ і ВМ для чотирьох арифметичних дій:
НМ(x+y)=НМx+НМy; ВМ(x+y)=ВМx+ВМy; НМ(x-y)=НМx - ВМy; ВМ(x-y)=ВМx - НМy;
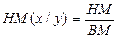 ;
;  НМ(xy)=НМx·НМy; ВМ(xy)=ВМx·ВМy;
НМ(xy)=НМx·НМy; ВМ(xy)=ВМx·ВМy;
Розглянемо приклад обчислень за методом меж.
Приклад. Батарея складається з трьох паралельно з’єднаних конденсаторів ємністю: С1=10±1мкФ, С2=2±0,2мкФ, С3=2±0,2мкФ. Знайдіть електроємність батареї С.
Так, як С1=10±1мкФ, то 9<С1<11, НМС1=9; ВМС1=11; НМС2=НМС3=1,8; ВМС2=ВМС3=2,2.
Для зручності обчислення меж складають таблицю:
| НМ | ВМ | |
| С1 | ||
| С2 | 1,8 | 2,2 |
| С3 | 1,8 | 2,2 |
| С4 | 12,6 | 15,4 |
 ;
; 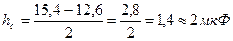 ; С=14±2 мкФ.
; С=14±2 мкФ.
Метод меж використовується для оцінки похибок результату при розв’язуванні задач і при виконанні лабораторних робіт.
2. Метод підрахунку цифр
Розглянутий метод меж належить до методу строгого врахування похибок, тобто дозволяє знайти межу абсолютної і відносної похибки результату, що на практиці далеко не завжди обов’язково. В багатьох випадках достатньо визначити число значущих без спеціального обчислення похибок, що значно спрощує хід обчислення.
Метод наближених обчислень, який дозволяє оцінити точність результату за кількістю цифр в компонентах носить назву методу підрахунку цифр.
Застосування цього методу ґрунтується на тому, що кількість правильних значущих цифр наближеного значення числа визначає відносну похибку: чим більше правильних значущих цифр в числі, тим менша його відносна похибка.
Метод підрахунку цифр являє собою систему, в якій операції над наближеними значеннями чисел виконуються загальновідомими способами і лише результат заокруглюють за спеціальними правилами – правилами підрахунку цифр.
Цей метод можна застосовувати тоді, коли якість приладів або метод проведення лабораторних робіт не дає можливості достовірно оцінити похибки вимірювань.
Метод підрахунку цифр полягає в наступному: результати вимірювань вираховують так, щоб в наближеному числі всі цифри були правильними і тільки остання – сумнівна; всі обчислення виконуємо за правилами наближених обчислень; кінцеву похибку обчислень оцінюють двома – трьома одиницями останнього розряду; зняті з мір і вимірювальних приладів результати вимірювань повинні мати не менше двох цифр.
Приклад. Лабораторна робота: “Вимірювання об’єму тіла”.
Необхідно виміряти об’єм бруска за його довжиною, шириною і висотою. Нехай шляхом вимірювання штангенциркулем отримані наступні дані:
| Довжина | А=6,2 мм |
| Ширина | В=4,4 мм |
| Висота | С=1,2 мм |
Обчислюємо площу основи і об’єм тіла, застосовуючи правила дії над наближеними числами:  ,
, 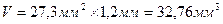 .
.
Дата добавления: 2014-12-03; просмотров: 600; Мы поможем в написании вашей работы!; Нарушение авторских прав |