Приклади. 1. Множина всіх натуральних чисел частково впорядкована, якщо означає „b ділиться на a без остачі”.

1. Множина всіх натуральних чисел частково впорядкована, якщо означає „b ділиться на a без остачі”.

2. Множина всіх підмножин деякої фіксованої множини частково впорядкована за включенням, якщо означає, що .

3. Упорядкованою парою (a , b) є множина .

Нехай a, b − елементи частково впорядкованої множини. Може виявитися, що жодне із співвідношень і 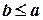не має місця. У цьому випадку елементи a, b називаються непорівнянними. Тобто відношення порядку може бути визначеним лише для деяких пар елементів, тому й говориться про часткову впорядкованість. Якщо ж в частково впорядкованій множині M непорівняних елементів немає, то множина M називається впорядкованою ( лінійно впорядкованою, цілком упорядкованою ).

Декартовим добутком множин називається множина впорядкованих 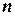-ок:

.

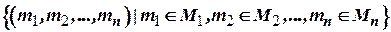Застосовується позначення .

ЛЕКЦІЯ 2

1. Поняття відображення або функції.

2. Потужність множин.

3. Зчисленні множини.

4. Математична індукція.