Зчисленні множини

Множина 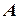називається зчисленною, якщо A ~ N. У цьому випадку говорять, що елементи множини 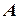можна занумерувати.

Мають місце наступні твердження:

1. Нескінченна підмножина зчисленної множини зчисленна.

2. Нескінченна множина містить зчисленну підмножину.

3. Об'єднання зчисленної множини зчисленних множин є зчисленною множиною.

4. Декартів добуток двох зчисленних множин зчисленний.

5. Існують незчисленні множини.

Доведення першого і другого твердження досить прості. Їх пропонується виконати самостійно. Спинимось на доведенні твердження 3.

Нехай - зчисленні множини. Тоді для кожного .

Елементи об'єднання цих множин можна подати у вигляді таблиці

… …

…………………………………………

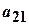
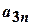і занумерувати, наприклад у порядку, вказаному стрілками. Цим саме буде встановлена бієкція . Отже, .

Аналогічно доводиться твердження 4.

Нехай . Тоді декартів добуток складається із пар, які можна розташувати в такому порядку

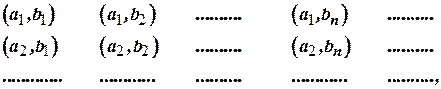
і занумерувати так, як зроблено в попередньому випадку.

Для доведення твердження 5 застосуємо діагональний метод (діагональну процедуру) Кантора.

Нехай 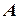− множина всіх можливих нескінченних ланцюгів, що складаються з двох символів, наприклад 0 і 1, вигляду

Покажемо, що множина 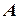незчисленна. Припустимо, що елементи множини 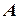занумеровані, тобто що множина 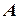зчисленна. Нехай

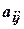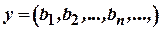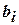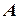де кожне дорівнює 0 або 1. Утворимо елемент , поклавши , і кожне відповідно дорівнює 0 або 1. Очевидно, що , але не збігається з жодним із занумерованих елементів . А це суперечить тому, що всі елементи множини можна занумерувати.