
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Деякі властивості дійсних чисел
Наведемо деякі властивості дійсних чисел.
1. Число 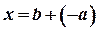 є розв'язком рівняння
є розв'язком рівняння 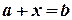 .
.
Доведення. Підставимо в дане рівняння замість 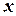 його значення:
його значення:
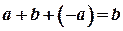 .
.
Згідно з 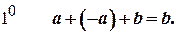
Згідно з 
Згідно з 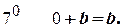
Згідно з 
Зауваження. Число  називається різницею чисел
називається різницею чисел 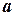 та
та  і позначається
і позначається  . Зазначимо, що за умови
. Зазначимо, що за умови 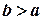 різниця
різниця  . Дійсно, якщо
. Дійсно, якщо 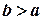 , то за
, то за  Одержуємо
Одержуємо 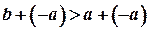 , далі за
, далі за  Маємо
Маємо 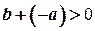 , тобто
, тобто  .
.
2. Число  є розв'язком рівняння
є розв'язком рівняння  , якщо
, якщо  .
.
Доведення. Підставимо в дане рівняння значення 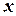 :
:
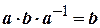 .
.
Згідно з  .
.
Згідно з 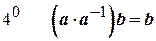 .
.
Згідно з  .
.
Згідно з  .
.
Зауваження. Число 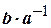 називається часткою чисел
називається часткою чисел 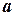 й
й  і позначається
і позначається  або
або 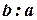 .
.
3. Якщо 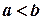 , то
, то  .
.
Дійсно, оскільки 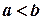 , то
, то  . Отже, за
. Отже, за 
 , звідки одержуємо
, звідки одержуємо  .
.
Зокрема, якщо 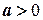 , то
, то 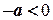 , а якщо
, а якщо 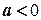 , то
, то  .
.
Дійсно, згідно з 
 , далі за
, далі за 
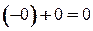 . Отже,
. Отже,
0= − 0.
4. Якщо 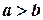 і
і 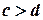 , то
, то  .
.
Дійсно, якщо 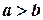 і
і 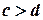 , то за
, то за 
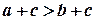 ,
, 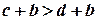 . Далі згідно з
. Далі згідно з 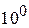
 .
.
5. Якщо 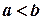 та
та 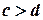 , то
, то  .
.
Дійсно, якщо 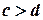 , то згідно з
, то згідно з 
 і за 4 одержуємо:
і за 4 одержуємо:  .
.
6. 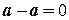 .
.
Це випливає з того, що  .
.
7.  .
.
Справді, 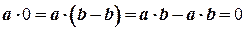 .
.
8.  .
.
Дана рівність доводиться так:  .
.
9. 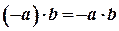 .
.
Доведення: 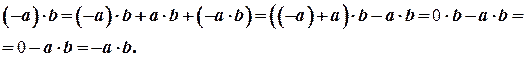
Зокрема,  .
.
10. Якщо 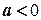 і
і  , то
, то 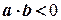 .
.
Дійсно, оскільки 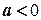 , то
, то  , а тому
, а тому  (згідно з
(згідно з 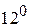 ). Отже,
). Отже,  , а звідси
, а звідси 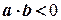 .
.
11. Якщо 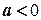 та
та 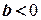 , то
, то  .
.
Справді, оскільки 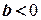 , то
, то  , а тому
, а тому  (згідно з
(згідно з 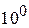 ). Отже,
). Отже,  , а звідси маємо
, а звідси маємо  .
.
12. Якщо  , то
, то  .
.
Це випливає з 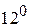 і 11.
і 11.
За властивістю 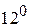 маємо:
маємо: 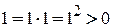 , тобто
, тобто 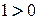 .
.
Надалі будемо використовувати й інші властивості дійсних чисел, не спиняючись на їх формальному доведенні.
Дата добавления: 2014-12-03; просмотров: 394; Мы поможем в написании вашей работы!; Нарушение авторских прав |