
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Межі числових множин
Нехай задано непорожню числову множину  .
.
Множина  називається обмеженою зверху, якщо існує таке дійсне число
називається обмеженою зверху, якщо існує таке дійсне число  , що для кожного
, що для кожного  виконується нерівність
виконується нерівність 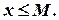
Множина  називається обмеженою знизу, якщо існує таке дійсне число
називається обмеженою знизу, якщо існує таке дійсне число  , що для кожного
, що для кожного  виконується нерівність
виконується нерівність 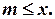
При цьому числа  і
і  називаються відповідно верхньою та нижньою межею множини
називаються відповідно верхньою та нижньою межею множини  .
.
Множина, яка обмежена зверху й знизу, називається обмеженою.
Очевидно, що будь-яка обмежена зверху (знизу) множина  має безліч верхніх (нижніх) меж.
має безліч верхніх (нижніх) меж.
Найменша верхня межа обмеженої зверху множини  називається точною верхньою межею або верхньою гранню цієї множини і позначається
називається точною верхньою межею або верхньою гранню цієї множини і позначається  (supremum (лат.) – найвище).
(supremum (лат.) – найвище).
Найбільша нижня межа обмеженої знизу множини  називається точною нижньою межею або нижньою гранню цієї множини і позначається
називається точною нижньою межею або нижньою гранню цієї множини і позначається  (infimum (лат.) – найнижче).
(infimum (лат.) – найнижче).
Якщо  , то для довільного числа
, то для довільного числа  існує
існує  таке, що
таке, що 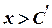 . Якщо
. Якщо  , то для довільного числа
, то для довільного числа  існує
існує  таке, що
таке, що 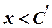 .
.
Теорема. Будь-яка непорожня обмежена зверху числова множина має точну верхню межу. Якщо ж вона обмежена знизу, то має точну нижню межу.
Доведення. Нехай  – непорожня обмежена зверху числова множина. Тоді множина
– непорожня обмежена зверху числова множина. Тоді множина  чисел, які обмежують
чисел, які обмежують  зверху, непорожня. Із означення верхньої межі випливає, що
зверху, непорожня. Із означення верхньої межі випливає, що  виконується нерівність
виконується нерівність 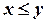 . За аксіомою неперервності дійсних чисел існує таке число
. За аксіомою неперервності дійсних чисел існує таке число  , що
, що  виконується нерівність
виконується нерівність  .
.
Із цієї нерівності випливає, що  обмежує
обмежує  зверху, тобто є верхньою межею, і є найменшим із усіх верхніх меж, тобто є точною верхньою межею.
зверху, тобто є верхньою межею, і є найменшим із усіх верхніх меж, тобто є точною верхньою межею.
Друга частина теореми доводиться аналогічно.
Якщо множина  не обмежена зверху ( знизу ), то за домовленістю пишуть
не обмежена зверху ( знизу ), то за домовленістю пишуть 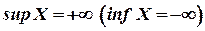 .
.
Дата добавления: 2014-12-03; просмотров: 541; Мы поможем в написании вашей работы!; Нарушение авторских прав |