Абсолютна величина числа позначається символом .

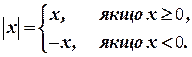
Із означення абсолютної величини випливає, що нерівності і , де рівносильні, тобто .

Теорема. Абсолютна величина суми двох чисел не більше від суми абсолютних величин чисел, тобто .

Доведення. За означення абсолютної величини

для будь-яких чисел . Додаючи почленно ці нерівності, одержимо

.

Остання нерівність рівносильна нерівності

.

Теорема. Абсолютна величина різниці двох чисел не менше від різниці абсолютних величин чисел, тобто

.

Доведення. Для будь-яких чисел маємо

За попередньою теоремою

.

Звідси одержуємо

.

Зазначимо, що мають місце співвідношення

ТЕМА 2. ЧИСЛОВІ ПОСЛІДОВНОСТІ

ЛЕКЦІЯ 5

1. Означення числової послідовності.

2. Арифметичні дії над числовими послідовностями.

3. Обмежені і необмежені числові послідовності.

4. Нескінченно малі і нескінченно великі послідовності.

5. Основні властивості нескінченно малих послідовностей.