Збіжні послідовності

Границя числової послідовності. Число 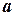називається границею послідовності , якщо для будь-якого числа 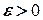існує такий номер , що для всіх членів послідовності із номером виконується нерівність

. (2)

Якщо число 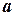є границею послідовності , то пишуть

,

а саму послідовність називають збіжною.

Послідовність, яка не є збіжною, називається розбіжною.

Приклад.Довести, що .

Доведення. Задамо довільне число 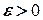і покажемо, що існує таке натуральне число , що для всіх членів послідовності із номером виконується нерівність .

Оскільки , то

.

Розв'язавши відносно 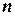нерівність , маємо .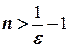

Якщо в значенні узяти цілу частину числа 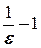, тобто покласти 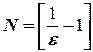, то нерівність <ε виконується для всіх . Отже, .

Якщо послідовність збіжна і , то будь-який її елемент можна подати у вигляді , де - елемент нескінченно малої послідовності .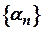

Дійсно, якщо , то послідовність є нескінченно малою, оскільки для будь-якого 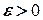існує такий номер , що для виконується нерівність , тобто .

Має місце й обернене твердження. Якщо можна подати у вигляді , де 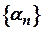- нескінченно мала послідовність, то .

Нерівність (2) рівносильна нерівності або ,

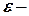із якої випливає, що знаходиться в околі точки 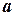. Отже, означення границі числової послідовності можна дати наступним чином.

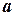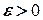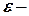Число називається границею послідовності , якщо для будь-якого числа існує такий номер , що всі члени послідовності із номером знаходяться в околі точки .

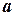Очевидно, що нескінченно велика послідовність не має границі. Іноді говорять, що вона має нескінченну границю і пишуть

.

Якщо при цьому, починаючи з деякого номера, всі члени послідовності додатні ( від'ємні ), то пишуть .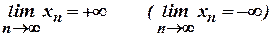

Усяка нескінченно мала послідовність збіжна, причому .

Це безпосередньо випливає з означення границі числової послідовності й означення нескінченно малої числової послідовності.