Приклади.

1. Якщо і , то .

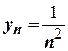2. Якщо і , то .

3. Якщо і , то .

4. Якщо і , то та не існує.

Отже, лише значення границь числових послідовностей , не дозволяє у розглянутому вище випадку робити висновки про значення границі їх відношення. Для того, щоб схарактеризувати цю особливість, говорять, що за умови 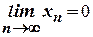і вираз є невизначеністю типу .

Аналогічно невизначеними виразами є:

а) у випадку і вираз є невизначеністю типу ;

б) у випадку 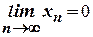і вираз є невизначеністю типу ;

в) у випадку та вираз є невизначеністю типу .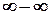

Для визначення границь невизначених виразів типу часто може застосовуватися теорема Штольца, яку ми наведемо без доведення

Теорема. Якщо послідовності 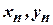такі, що

1) починаючи з деякого номера

2) ;

3) існує

то .

ЛЕКЦІЯ 7

9. Граничний перехід у нерівностях.

10. Монотонні послідовності.

11. Число е.

12. Теорема про вкладені відрізки.