
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Граничний перехід у нерівностях
Теорема . Якщо елементи збіжної послідовності  , починаючи з деякого номера
, починаючи з деякого номера 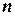 , задовольняють нерівність
, задовольняють нерівність  , то і границя цієї послідовності задовольняє нерівність
, то і границя цієї послідовності задовольняє нерівність 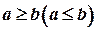 .
.
Доведення. Нехай, починаючи з деякого номера 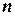 , елементи збіжної послідовності
, елементи збіжної послідовності  задовольняють нерівність
задовольняють нерівність  і
і  . Припустимо, що
. Припустимо, що 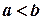 . Оскільки
. Оскільки  , то для
, то для  існує номер
існує номер  такий, що для
такий, що для  виконується нерівність
виконується нерівність  , яка рівносильна нерівності
, яка рівносильна нерівності  . Тоді із нерівності
. Тоді із нерівності  одержуємо:
одержуємо:  , що суперечить умові. Отже,
, що суперечить умові. Отже,  .
.
Випадок  доводиться аналогічно.
доводиться аналогічно.
Наслідок 1. Якщо елементи збіжних послідовностей  і
і  , починаючи з деякого номера
, починаючи з деякого номера 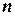 , задовольняють нерівність
, задовольняють нерівність  , то
, то  .
.
Нехай, починаючи з деякого номера, виконується нерівність  . Тоді для таких
. Тоді для таких 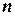
 . Отже,
. Отже,  , а тому
, а тому  . Звідси маємо
. Звідси маємо  . Другий випадок установлюється аналогічно.
. Другий випадок установлюється аналогічно.
Теорема. Нехай члени послідовностей  ,
,  ,
,  , починаючи з деякого номера, задовольняють нерівність
, починаючи з деякого номера, задовольняють нерівність  і
і  . Тоді послідовність
. Тоді послідовність  збіжна й
збіжна й 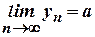 .
.
Доведення. Задамо довільне число 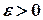 . Тоді для заданого
. Тоді для заданого 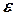 знайдеться такий номер
знайдеться такий номер  , що для
, що для  виконуватиметься нерівність
виконуватиметься нерівність  , тобто
, тобто  . Для цього ж
. Для цього ж 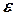 знайдеться такий номер
знайдеться такий номер  , що
, що  для
для  , тобто
, тобто  .
.
Виберемо  . Тоді виконуватиметься нерівність
. Тоді виконуватиметься нерівність
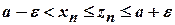
для всіх  .
.
Ураховуючи умову теореми, маємо 
або  , тобто
, тобто  для всіх
для всіх  . Звідси випливає, що
. Звідси випливає, що 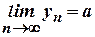 .
.
Дата добавления: 2014-12-03; просмотров: 603; Мы поможем в написании вашей работы!; Нарушение авторских прав |