Нескінченно малі і нескінченно великі послідовності.

Послідовність називається нескінченно великою, якщо для будь-якого числа існує такий номер , що для всіх елементів із номером виконується нерівність .

Зауваження. У наведеному означенні номер залежить від числа 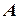, тобто .

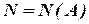Очевидно, що всяка нескінченно велика послідовність є необмеженою, проте не всяка необмежена послідовність є нескінченно великою. Наприклад, необмежена послідовність 0, 1, 0, 2, 0, 3, ..., n, 0, n+1, … не є нескінченно великою, оскільки не існує такого номера , щоб для всіх , де виконувалася б, наприклад, нерівність .

Послідовність 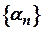називається нескінченно малою, якщо для будь-якого (як завгодно малого) числа 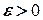існує такий номер , що для всіх елементів із номером виконується нерівність .

Зауваження. У наведеному означенні номер залежить від числа 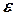, тобто .

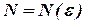Приклад 1. Показати, що послідовність є нескінченно великою.

Нехай маємо довільне число . Із нерівності 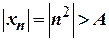або .

Покладемо .

Тоді . Оскільки , то 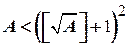. Отже, при виконується нерівність .

Приклад 2. Показати, що послідовність є нескінченно малою.

Нехай маємо довільне число 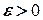. Із нерівності одержуємо . Покладемо . Тоді для всіх маємо , тобто або .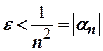

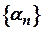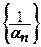Теорема. Якщо - нескінченно велика послідовність і всі її члени відмінні від нуля, то послідовність нескінченно мала, і, навпаки, якщо - нескінченно мала послідовність й , то послідовність нескінченно велика.

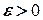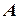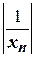Доведення. Нехай - нескінченно велика послідовність. Візьмемо довільне і покладемо . Оскільки нескінченно велика послідовність, то для вказаного існує номер такий, що при виконується нерівність . Звідси маємо . Отже, послідовність - нескінченно мала.

Друга частина теореми доводиться аналогічно.