
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Властивості збіжних послідовностей
ТеоремаЗбіжна послідовність має єдину границю.
Доведення. Припустимо, що збіжна послідовність  має дві різні границі
має дві різні границі 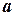 і
і  , тобто
, тобто  . Тоді
. Тоді  та
та  , де
, де  і
і 
 - елементи нескінченно малих послідовностей
- елементи нескінченно малих послідовностей 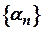 та
та 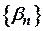 . Отже,
. Отже,  або
або 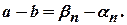 Оскільки
Оскільки  , за властивістю нескінченно малих послідовностей, є елементами нескінченно малої послідовності, а
, за властивістю нескінченно малих послідовностей, є елементами нескінченно малої послідовності, а  постійне число, то
постійне число, то  . Таким чином,
. Таким чином,  .
.
Теорема. Якщо послідовність  збіжна, то вона обмежена.
збіжна, то вона обмежена.
Доведення. Нехай  і
і 
 - номер, починаючи з якого виконується нерівність
- номер, починаючи з якого виконується нерівність  , де
, де 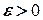 . Тоді
. Тоді

для всіх  . Виберемо
. Виберемо  . За цієї умови
. За цієї умови  для будь-якого
для будь-якого  .
.
Зазначимо, що не всяка обмежена послідовність є збіжною. Наприклад, послідовність  обмежена, але не збіжна.
обмежена, але не збіжна.
Теорема 2.6. Якщо  і
і  - збіжні послідовності, то:
- збіжні послідовності, то:
1. Послідовність  , яка є сумою (різницею) збіжних послідовностей
, яка є сумою (різницею) збіжних послідовностей  та
та  , збіжна і її границя дорівнює сумі (різниці) границь цих послідовностей, тобто
, збіжна і її границя дорівнює сумі (різниці) границь цих послідовностей, тобто 
 .
.
2. Послідовність 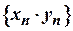 , яка є добутком збіжних послідовностей
, яка є добутком збіжних послідовностей  й
й  , збіжна і її границя дорівнює добутку границь цих послідовностей, тобто
, збіжна і її границя дорівнює добутку границь цих послідовностей, тобто 
 .
.
3. Послідовність  , яка є часткою збіжних послідовностей
, яка є часткою збіжних послідовностей  та
та  , за умови
, за умови  , збіжна і її границя дорівнює частці границь цих послідовностей, тобто
, збіжна і її границя дорівнює частці границь цих послідовностей, тобто  .
.
Доведення. Нехай  і
і  - збіжні послідовності та
- збіжні послідовності та 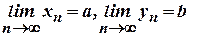 . Тоді
. Тоді  і
і  , де
, де  й
й  – елементи нескінченно малих послідовностей
– елементи нескінченно малих послідовностей 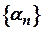 і
і 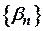 . Покажемо, що має місце:
. Покажемо, що має місце:
1)  .
.
Оскільки 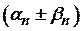 є елементами нескінченно малої послідовності
є елементами нескінченно малої послідовності  , то звідси випливає, що
, то звідси випливає, що  .
.
2)  .
.
Оскільки  є елементами нескінченно малої послідовності
є елементами нескінченно малої послідовності  , то
, то  .
.
Тобто  .
.
3) 


Послідовність  є нескінченно малою. Покажемо, що послідовність
є нескінченно малою. Покажемо, що послідовність  обмежена. Оскільки
обмежена. Оскільки 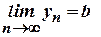 і
і  , то для
, то для 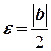 існує такий номер
існує такий номер  , що для всіх
, що для всіх  виконується нерівність
виконується нерівність  ,
,
отже,  , тобто
, тобто  , а тому
, а тому  для всіх
для всіх  . Звідси випливає, що послідовність
. Звідси випливає, що послідовність  обмежена.
обмежена.
Таким чином, послідовність  нескінченно мала, а тому
нескінченно мала, а тому
 ,
,
тобто
 , де
, де  .
.
Зауваження. Пункт 1) наведеної теореми допускає узагальнення на довільне скінченне число доданків. Пункт 2) - на довільне скінченне число множників. Із пункту 2) випливає, що постійний множник можна виносити за знак границі, тобто
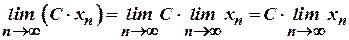 .
.
Дата добавления: 2014-12-03; просмотров: 388; Мы поможем в написании вашей работы!; Нарушение авторских прав |