Дійсні числа

Уведемо аксіоматичне означення дійсних чисел. Із шкільного курсу математики відомо, що множина дійсних чисел складається із множини раціональних та ірраціональних чисел. Раціональним називається число, яке можна подати у вигляді звичайного дробу 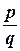, де p, q − цілі числа, причому . Ірраціональним називається число, яке не є раціональним. Будь-яке раціональне число є або цілим, або скінченним чи нескінченним періодичним десятковим дробом. Ірраціональні числа – це нескінченні періодичні десяткові дроби. Виявлення ірраціональних чисел пов'язане з установленням у школі Піфагора (570-496 р. до н. е.) несумірності діагоналі квадрата і його сторони, тобто з установленням того факту, що довжина діагоналі квадрата не може бути виражена раціональним числом, якщо в значенні одиниці вимірювання взяти довжину сторони квадрата.

Ми дамо аксіоматичне означення множини дійсних чисел.

Множиною дійсних чисел називається множина елементів, для яких виконуються наступні аксіоми.