Поняття відображення або функції

Нехай X і Y дві множини. Відображенням f множини X у множину Y називається правило, яке кожному елементу ставить у відповідність один і тільки один елемент .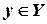

Замість слова "відображення" можна вживати "функція", "оператор", "відповідність".

Записи 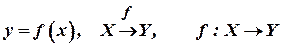означають, що f є відображенням множини X у множину Y.

Для позначення функції вживаються й інші букви, наприклад .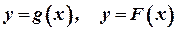

Елемент y, який відображення f ставить у відповідність елементу 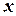, називається образом елемента 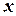при відображенні f або значенням відображення f у точці 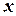і позначається символом . Множина X називається областю визначення відображення f і позначається 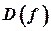. Множина 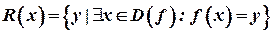називається множиною значень відображення f.

Нехай 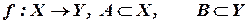. Образом множини A при відображенні f називається множина 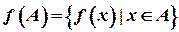. Прообразом множини при відображенні називається множина .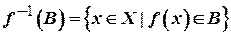

Графіком функції 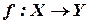називається множина .

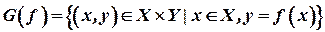Якщо 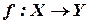і 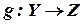, то функція 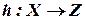, яка визначається формулами 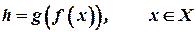називається складеною функцією, або суперпозицією функцій f і g.

Приклади.

Відображення 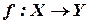називається відображенням множини Х на множину або сур'єкцією, якщо .

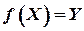Відображення 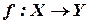називається взаємооднозначним відображенням множини X у множину Y або ін'єкцією, якщо

Відображення 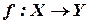, яке є сур'єкцією та ін'єкцією, називається бієкцією. У цьому випадку говорять, що здійснює взаємно однозначну відповідність між множинами і .

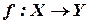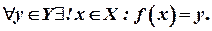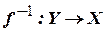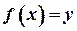Якщо − бієкція, то Функція називається оберненою до бієкції , якщо та .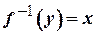

Відображення 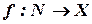називається послідовністю елементів із . Послідовність позначається так: 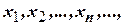де 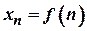− 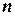-ний член послідовності.