Лекція 18

1. Розглянувши геометричні образи рівнянь першого степеня на площині та в просторі (пряма та площина), зупинимось на дослідженні рівнянь другого степеня.

Загальне рівняння другого степеня відносно змінних та можна записати у виді

, (1)

де хоча б один із коефіцієнтів a, b та c відмінний від нуля. З окремими випадками таких рівнянь ми уже зустрічалися, розглядаючи рівняння (коло з центром у точці , радіус якого дорівнює ), (парабола, вісь якої паралельна до осі ), (або , рівностороння гіпербола, дві вітки якої розташовані в першій та третій або другій та четвертій координатних четвертях). Проте наведені приклади не вичерпують всі можливі випадки ліній, які задаються рівнянням (1). Наприклад, рівняння визначає дві прямі, які перетинаються. У цьому легко переконатися, перетворивши рівняння до виду . Рівняння має єдиний розв’язок , що стає очевидним, якщо його записати у виді 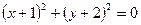. Рівняння або взагалі не задовольняє жодна пара дійсних чисел.

Скільки та які типи ліній визначає рівняння (1), ми дослідимо дещо пізніше (лекції 18 – 22), а поки що розглянемо деякі лінії, рівняння яких можна отримати, як частинні випадки рівняння (1).

2. Еліпс. Розглянемо на площині дві точки та , відстань між якими позначимо 2с та поставимо задачу відшукання геометричного місця всіх точок, сума відстаней від кожної з яких до точок та є сталою, яка дорівнює деякому числу 2а. Будемо вважати, що , оскільки при шукана множина точок буде порожньою, а при утворить відрізок .

Означення 1. Множина всіх точок площини, сума відстаней від кожної з яких до двох фіксованих точок та є сталою величиною, яка більша від довжини відрізка , називається еліпсом.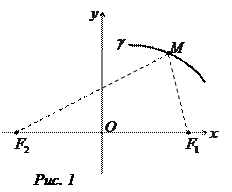

Точки та називаються фокусами еліпса. Щоб скласти рівняння еліпса, введемо прямокутну декартову систему координат , вибравши за точку середину відрізка та прийнявши пряму за вісь (рис.1). Фокуси еліпса відносно введеної системи координат матимуть координати F₁(c;0), F₂(-c;0). Нехай M(x;y) - одна із точок шуканого геометричного місця . Тоді, згідно з означенням еліпса,

. (2)

Скориставшись формулою відстані між двома точками, дістаємо

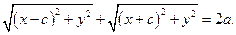
Для спрощення одержаного співвідношення, запишемо його у виді

,

звідки

,

або

(3)

Підносячи до квадрату обидві частини одержаної рівності, отримуємо

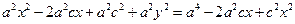(4)

або

. (5)

Оскільки a>c, то вираз 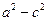додатній, тому, ввівши заміну 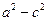= та розділивши рівність (5) на , дістаємо

(6)

Отже, координати кожної точки на еліпсі задовольняють рівняння (6). Покажемо, що кожен розв’язок рівняння (6) задає точку на еліпсі. Нехай – розв’язок рівняння (6) та М(x; y) - відповідна точка. Тоді пара чисел (x;y) задовольняє рівняння (5) та (4). Запишемо рівняння (4) у виді 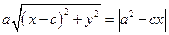, звідки випливає, що

.

Очевидно, що для розв’зків рівняння (6) повинна виконуватись умова (якщо , то 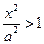і рівність (6) неможлива). Оскільки , то , тому вираз - додатній. Таким чином,

. (7)

Міркуючи аналогічно, дістаємо

. (8)

Тому , тобто точка М належить еліпсу. Таким чином, доведено, що рівняння (6) є рівнянням еліпса. Його називають канонічним рівнянням еліпса.

Рівняння є рівнянням другого степеня, тому еліпс – це лінія другого порядку. Відрізки та називають фокальними радіусами точки М. Співвідношення (7), (8) дозволяють обчислювати довжини фокальних радіусів, знаючи тільки абсцису точки, яка належить еліпсу.

3. Гіпербола. Нехай на площині задані точки та та . Знайдемо геометричне місце точок площини, модуль різниці відстаней від кожної з яких до точок та є сталою величиною, яка дорівнює заданому числу 2а.

Лекція 18