
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пряма на площині. Різні способи задання прямої на площині.
План.
Геометричні образи рівняння першого степеня з двома змінними.
Різні способи задання прямої на площині.
Частинні випадки загального рівняння прямої.
Приклади.
Дослідимо, які геометричні образи відповідають рівнянню першого степеня з двома змінними, тобто рівнянню , в якому хоча б один із коефіцієнтів біля змінних та відмінний від нуля (цю умову записують у виді або ). Покажемо, що в довільній афінній системі координат рівняння першого степеня
 (1)
(1)
визначає деяку пряму. Нехай 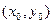 - фіксований та
- фіксований та  - довільний розв’язки рівняння (1). Віднімаючи від рівняння (1) рівність
- довільний розв’язки рівняння (1). Віднімаючи від рівняння (1) рівність  , дістаємо
, дістаємо 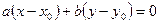 . Одержану рівність можна записати у виді
. Одержану рівність можна записати у виді
 ,
,  (2)
(2)
(тут  – деяке число). Введемо в розгляд точки
– деяке число). Введемо в розгляд точки  ,
,  та вектор
та вектор  . Тоді співвідношення (2) можна замінити векторною рівністю
. Тоді співвідношення (2) можна замінити векторною рівністю  . Оскільки для кожної точки
. Оскільки для кожної точки  вектор
вектор  залишається колінеарним сталому вектору
залишається колінеарним сталому вектору  , то всі такі точки належать прямій, що проходить через точку
, то всі такі точки належать прямій, що проходить через точку  та паралельна вектору
та паралельна вектору  .
.
Розглянемо основні способи задання прямої на площині.

|
 задана на координатній площині точкою
задана на координатній площині точкою  та паралельним до неї вектором
та паралельним до неї вектором  (рис. 1). Такий вектор називають напрямним вектором прямої. Тоді для довільної точки
(рис. 1). Такий вектор називають напрямним вектором прямої. Тоді для довільної точки  на прямій із колінеарності векторів
на прямій із колінеарності векторів  та
та  випливає, що
випливає, що  , або в координатній формі
, або в координатній формі 
 , звідки
, звідки
 (3)
(3)
Очевидно, що одержане рівняння є рівнянням першого степеня. Його називають канонічним рівнянням прямої.
Нехай пряма задана двома точками  та
та 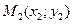 .Для того, щоб скласти її рівняння, скористаємось співвідношенням (3), замінивши точку
.Для того, щоб скласти її рівняння, скористаємось співвідношенням (3), замінивши точку  точкою
точкою  , та взявши замість вектора
, та взявши замість вектора  вектор
вектор  . Отримуємо
. Отримуємо
 . (4)
. (4)
Одержане рівняння називають рівнянням прямої, що проходить через дві задані точки.
Прирівнявши відношення в рівності (3) до параметра  , отримаємо
, отримаємо  ,
,  , звідки
, звідки
 . (5)
. (5)
Дані рівності називають параметричними рівняннями прямої. Якщо напрямний вектор  - одиничний, тобто
- одиничний, тобто 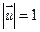 , то із рівності (5) дістанемо
, то із рівності (5) дістанемо
 ,
,
тобто у цьому випадку модуль параметра  має цілком конкретний геометричний зміст - це відстань між точками
має цілком конкретний геометричний зміст - це відстань між точками  та
та  на заданій прямій.
на заданій прямій.
 Нехай пряма d відтинає на координатних осях
Нехай пряма d відтинає на координатних осях  та
та  відрізки з довжинами
відрізки з довжинами  та
та  (рис. 2). Тоді на прямій будуть відомі дві точки
(рис. 2). Тоді на прямій будуть відомі дві точки  та
та  і ми можемо скористатись рівністю (2). Дістаємо
і ми можемо скористатись рівністю (2). Дістаємо  , або
, або 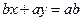 . Розділивши одержану рівність на
. Розділивши одержану рівність на  , дістанемо
, дістанемо
 . (6)
. (6)
Одержане співвідношення називають рівнянням прямої у відрізках на осях.
 Нехай система координат прямокутна декартова, а пряма d задається в ній точкою
Нехай система координат прямокутна декартова, а пряма d задається в ній точкою  та перпендикулярним до неї вектором
та перпендикулярним до неї вектором  (рис. 3). Такий вектор називають вектором нормалі до прямої або нормальним вектором. Точка
(рис. 3). Такий вектор називають вектором нормалі до прямої або нормальним вектором. Точка  належить прямій d тоді і тільки тоді, коли вектори
належить прямій d тоді і тільки тоді, коли вектори  та
та  будуть перпендикулярні, тобто тоді і тільки тоді, коли їхній скалярний добуток рівний нулю. З рівності
будуть перпендикулярні, тобто тоді і тільки тоді, коли їхній скалярний добуток рівний нулю. З рівності 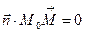 дістаємо
дістаємо
 (7)
(7)
Одержане співвідношення називають рівнянням прямої, що проходить через задану точку перпендикулярно до даного напрямку.
Нехай пряма  утворює з додатнім напрямком осі Ох кут
утворює з додатнім напрямком осі Ох кут  ( система координат вважається прямокутною декартовою) та проходить через точку
( система координат вважається прямокутною декартовою) та проходить через точку 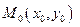 (рис. 4). Знайдемо напрямний вектор
(рис. 4). Знайдемо напрямний вектор  до прямої
до прямої  . Очевидно що за допомогою кута
. Очевидно що за допомогою кута  його координати можна виразити рівностями
його координати можна виразити рівностями 
 . Скориставшись рівнянням (3), дістанемо
. Скориставшись рівнянням (3), дістанемо  , звідки
, звідки

 , (8)
, (8)
або
 , (
, (  )
)
де  . Рівняння (8) або (
. Рівняння (8) або (  ) називають рівнянням прямої з кутовим коефіцієнтом. Кутовий коефіцієнт
) називають рівнянням прямої з кутовим коефіцієнтом. Кутовий коефіцієнт  визначає кут нахилу прямої до осі
визначає кут нахилу прямої до осі  . Очевидно, що рівняння прямих, які перпендикулярні до осі
. Очевидно, що рівняння прямих, які перпендикулярні до осі  , у вигляді (8) подати не можна.
, у вигляді (8) подати не можна.
Розглянуті нами вище варіанти різних способів задання прямої в усіх випадках проводять до рівняння прямої у виді (1). Тому рівняння  називають загальним рівнянням прямої.
називають загальним рівнянням прямої.
В якому виді записувати рівняння прямої залежить від задачі, яка розв’язується. Наприклад, якщо трикутник заданий координатами своїх вершин, то рівняння медіан легко отримати, користуючись рівнянням прямої, що проходить через дві точки. Для того, щоб скласти рівняння висот, доцільно використовувати рівняння прямої, що проходить через дану точку перпендикулярно до заданого вектора. В ролі останнього досить взяти вектор, який сполучає дві інші вершини трикутника. При написанні рівняння бісектриси трикутника можна скористатися її напрямним вектором  , або
, або  де
де  - вектори, які побудовані на сторонах трикутника і виходять із спільної вершини. В обох випадках вектор
- вектори, які побудовані на сторонах трикутника і виходять із спільної вершини. В обох випадках вектор  , як вектор суми двох рівних за довжиною векторів, співпадає з діагоналлю ромба, яка, як відомо, є бісектрисою його кута.
, як вектор суми двох рівних за довжиною векторів, співпадає з діагоналлю ромба, яка, як відомо, є бісектрисою його кута.
Водночас зауважимо, що у виді (3) не записують рівняння прямих, якщо одна із координат напрямного вектора рівна 0. У виді (4) не записують рівняння прямих, що проходять через дві точки з рівними абсцисами або ординатами. У вигляді (8) не можна записати рівняння прямих, які перпендикулярні до осі  .
.
3. Розглянемо частинні випадки рівняння (1), коли деякі із коефіцієнтів рівняння рівні нулю. Отже, нехай рівняння прямої задано у виді  .
.
При  рівняння прямої запишеться у вигляді
рівняння прямої запишеться у вигляді  . Очевидно, що пряма проходить через початок координат.
. Очевидно, що пряма проходить через початок координат.
Нехай  . Рівняння прямої запишеться у вигляді
. Рівняння прямої запишеться у вигляді  і, оскільки
і, оскільки  (рівняння прямої є рівнянням першого степеня, тому
(рівняння прямої є рівнянням першого степеня, тому  та
та  одночасно не можуть дорівнювати нулю), то
одночасно не можуть дорівнювати нулю), то  В цьому випадку для всіх точок прямої ординати рівні
В цьому випадку для всіх точок прямої ординати рівні  , а абсциси
, а абсциси  довільні, тому пряма проходить через точку
довільні, тому пряма проходить через точку  на осі
на осі  паралельно до осі
паралельно до осі  . Якщо
. Якщо  ,то пряма
,то пряма  проходить через початок координат і паралельна до осі
проходить через початок координат і паралельна до осі  , тобто рівняння
, тобто рівняння  є рівнянням осі Ох.
є рівнянням осі Ох.
Аналогічно, при  рівняння прямої запишеться у виді
рівняння прямої запишеться у виді 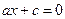 або
або  і визначає пряму, яка проходить через точку
і визначає пряму, яка проходить через точку  на осі
на осі  та паралельна до осі
та паралельна до осі  . При
. При  дістанемо рівняння
дістанемо рівняння 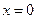 , яке є рівнянням осі
, яке є рівнянням осі  .
.
Зауважимо, що в загальному рівнянні прямої  коефіцієнти біля змінних х та у мають конкретний геометричний зміст: вони визначають координати вектора, який паралельний до прямої – це вектор
коефіцієнти біля змінних х та у мають конкретний геометричний зміст: вони визначають координати вектора, який паралельний до прямої – це вектор  , а у випадку прямокутної декартової системи координат вектор
, а у випадку прямокутної декартової системи координат вектор  перпендикулярний до прямої.
перпендикулярний до прямої.
4. Наведемо приклади задач, які розв’язуються за допомогою отриманих вище співвідношень.
 Задача 1. Довести, що медіани трикутника перетинаються в одній точці та діляться нею у відношенні
Задача 1. Довести, що медіани трикутника перетинаються в одній точці та діляться нею у відношенні  , рахуючи від вершини.
, рахуючи від вершини.
|
 (рис.5). Тоді точки
(рис.5). Тоді точки  ,
,  та
та  будуть серединами сторін
будуть серединами сторін 
 та
та  відповідно. Складемо рівняння медіан
відповідно. Складемо рівняння медіан  та
та  , користуючись рівнянням прямої у відрізках на осях. Дістаємо
, користуючись рівнянням прямої у відрізках на осях. Дістаємо 
 або
або 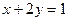 ,
, 
 або
або  . Нехай прямі перетинаються у точці
. Нехай прямі перетинаються у точці 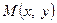 . Її координати ми знайдемо із системи
. Її координати ми знайдемо із системи  , розв’язуючи яку, дістаємо
, розв’язуючи яку, дістаємо  . Рівняння медіани
. Рівняння медіани  можна шукати у виді
можна шукати у виді 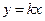 , оскільки пряма
, оскільки пряма  проходить через початок координат і не співпадає з віссю
проходить через початок координат і не співпадає з віссю  . Підставляючи координати точки
. Підставляючи координати точки  , дістаємо
, дістаємо 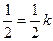 , тобто
, тобто  . Отже, рівняння медіани
. Отже, рівняння медіани  має вигляд
має вигляд  . Підставляючи знайдені вище координати точки
. Підставляючи знайдені вище координати точки  в одержане рівняння, переконуємось у тому, що точка
в одержане рівняння, переконуємось у тому, що точка  належить медіані
належить медіані  , тобто медіани перетинаються в одній точці. Порівнюючи координати векторів
, тобто медіани перетинаються в одній точці. Порівнюючи координати векторів 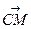 та
та 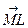 , бачимо, що
, бачимо, що  . Аналогічно встановлюємо, що
. Аналогічно встановлюємо, що  ,
,  . Задача розв’язана. Зауважимо, що в лекції 4 ми наводили векторний спосіб розв’язання даної задачі. Те, що ми ще раз повернулися до неї зроблено тільки з метою показати нові можливі способи її розв’язання методами аналітичної геометрії.
. Задача розв’язана. Зауважимо, що в лекції 4 ми наводили векторний спосіб розв’язання даної задачі. Те, що ми ще раз повернулися до неї зроблено тільки з метою показати нові можливі способи її розв’язання методами аналітичної геометрії.
Задача 2. Знайти ортоцентр (точку перетину висот) трикутника з вершинами у точках  ,
,  , та
, та 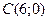 .
.
Розв’язання. Рівняння висоти  складемо, знаючи вершину А та знайшовши вектор
складемо, знаючи вершину А та знайшовши вектор  , який перпендикулярний до висоти
, який перпендикулярний до висоти  . Скориставшись співвідношенням (7), дістаємо
. Скориставшись співвідношенням (7), дістаємо  або
або  Аналогічно, знайшовши вектор
Аналогічно, знайшовши вектор  , дістаємо рівняння висоти
, дістаємо рівняння висоти  :
:  або
або  . Ортоцентр (точку
. Ортоцентр (точку  ) знаходимо, розв’язавши систему рівнянь
) знаходимо, розв’язавши систему рівнянь 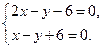
Відповідь:  .
.
Задача 3. Знайти сторону квадрата, вписаного в прямокутний трикутник з катетами 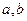 , знаючи, що дві сторони квадрата належать катетам трикутника.
, знаючи, що дві сторони квадрата належать катетам трикутника.
Розв’язання. Нехай сторона квадрата рівна  . Введемо в розгляд систему координат, вибравши початок координат у вершині прямого кута та спрямувавши координатні осі вздовж катетів трикутника. Скориставшись рівнянням прямої у відрізках на осях, запишемо рівняння гіпотенузи у виді
. Введемо в розгляд систему координат, вибравши початок координат у вершині прямого кута та спрямувавши координатні осі вздовж катетів трикутника. Скориставшись рівнянням прямої у відрізках на осях, запишемо рівняння гіпотенузи у виді  Оскільки вершина квадрата, яка належить гіпотенузі, має координати
Оскільки вершина квадрата, яка належить гіпотенузі, має координати  то виконується рівність
то виконується рівність  звідки
звідки  .
.
Відповідь:  .
.
Дата добавления: 2014-12-03; просмотров: 1312; Мы поможем в написании вашей работы!; Нарушение авторских прав |