Складання різницевого рівняння

В зв’язку з тим, що досліджувані процеси є періодичними, для знаходження умов стійкості необхідно вирішити на періоді роботи перетворювача, що передбачає складання різницевого рівняння. Різницеве рівняння роботи перетворювача має наступну форму:

Х((m+1)T) = HX(mT). (16)

Введемо позначення:

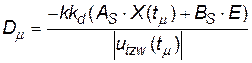. (17)

Тоді формула (15) матиме такий вигляд:

. (18)

Для розрахунку похідної u_tzw в точці t_μ необхідно визначити усталений процес в перетворювачі. Для цього необхідно знайти розв’язок рівняння (18) на одному періоді роботи перетворювача. Так як аналіз стійкості здійснюється в усталеному режимі, то момент комутації не залежить від номеру періода t_m = t₁. На першому інтервалі mT ≤ t ≤ mT+t₁ в момент часу t_μ=mT диференційне рівняння (18) має такий вид:

, (19)

де .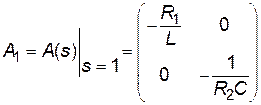

Позначимо 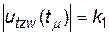і з врахуванням значень матриць А_S(s) і В_S(s) запишемо в явному вигляді вираз для вектора:

. (20)

Розв’яжемо рівняння (19) за допомогою перетворення Лапласа. Зображення рівняння (19) з урахуванням початкових умов Х_ξ(mT):

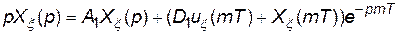. (21)

Зробимо заміну ,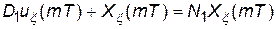

де .

З урахуванням цього рівняння (21) має наступний вигляд:

. (22)

Оригінал останнього виразу представляється за допомогою матричної експоненти:

. (23)

Підставляючи в цей вираз значення часу, що відповідає кінцю інтервалу постійності структури t=mT+t₁, отримаємо:

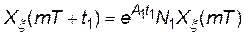. (24)

Аналогічно визначається рішення на другому інтервалі роботи перетворювача:

, (25)

де ,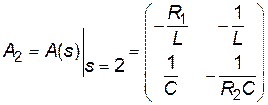

,

.

Підставляючи в оригінал час, що відповідає кінцю періода t = (m+1)T, отримаємо:

. (26)

Знаючи рішення (24) і (26), можна скласти різницеве рівняння, за яким здійснюється аналіз стійкості системи:

. (27)

Якщо розв’язок лінеаризованого рівняння (27) є стійким, то буде стійким в малому лінеаризована система в цілому.