Основи теорії хаосу

Теорія хаосу – це математичний апарат, який описує деякі нелінійні динамічні системи, поведінка яких дуже чутлива до початкових умов. Математичні системи з хаотичною поведінкою є детермінованими, тобто описуються деяким законом і в певному смислі є впорядкованими.

Засновниками теорії хаосу є французький вчений Анрі Пуанкаре, радянські математики Колмогоров А.М., Арнольд В.І. Для дослідження хаотичних систем використовують зображення у фазовому просторі, що дозволяє спростити виявлення хаотичних систем. Фазові траєкторії дисипативних систем (з втратами) завжди сходяться з часом в точку, яка відповідає стану спокою з мінімумом енергії – (0,0).

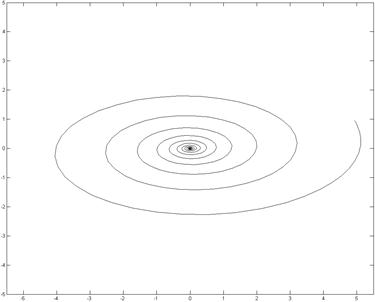
Рис. 1. Фазовий портрет дисипативної системи

В системах без втрат стаціонарна траекторія системи відповідає точці або замкненій траекторії.

Рис. 2. Фазовий портрет системи без втрат

Для позначення траекторії системи у стаціонарному режимі використовують термін атрактор. Більшість типів руху описується простими атракторами, які є обмеженими циклами. Хаотичний рух описується дивними атракторами. Однією з найпростіших неперервних систем, в яких може виникати хаотичний рух є система Лоренца, що описується системою з трьох нелінійних диференційних рівнянь:

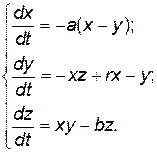(1)

Фазовий портрет системи Лоренца при початкових а = 10, r = 27, b = 8/3 показано на рис. 3.

Рис. 3. Дивний атрактор системи Лоренца

Хаотичні процеси можуть виникати лише в нелінійних системах. Якщо система неперервна вона має бути третього або вище порядку. У випадку дискретних систем, до яких відносяться імпульсні перетворювачі електроенергії, хаотичний руж може спостерігатись також і в системах першого та другого порядків.

Зміну поведінки системи доцільно розглядати відносно зміни деякого параметра. Якщо при його зміні виникає якісна зміна фазового портрету, говорять, що в системі виникає біфуркація, а точка в якій вона виникає називають точкою біфуркації. Приклад біфуркаційної діаграми для логістичного відображення:

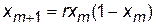, (2)

показаний на рис. 4.

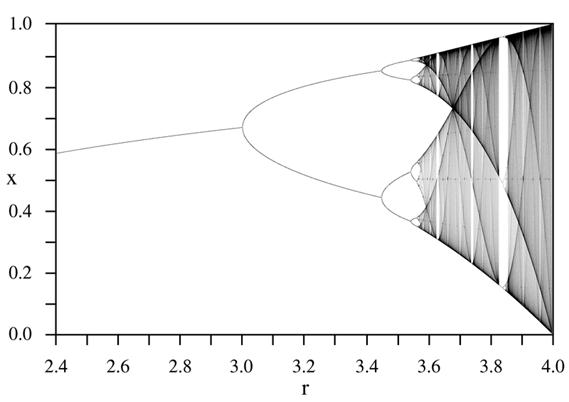
Рис. 4. Біфуркаційна діаграма для логістичного зображення

З біфуркаційної діаграми видно, що точка r = 3 є точкою біфуркації, після проходження якої період руху збільшується вдвічі. Подальше збільшення параметра r призводить до подальшого збільшення періоду і виникнення хаотичного руху.

Ще одним ефективним прийомом при дослідження детермінованого хаосу є переріз Пуанкаре, що представляє собою площину, яка перетинає фазовий портрет системи. Тому при використанні перерізу Пуанкаре здійснюється перехід системи з неперервним часом до системи з дискретним часом. Ще одним способом побудови перерізу Пуанкаре є розрахунок рівнянь системи в певні моменти часу t = mT+t_m. Якщо рух системи є періодичним на перерізі Пуанкаре присутня лише одна точка. У випадку виникнення субгармонійних коливань з періодом 2Т, на перерізі Пуанкаре присутні дві точки (для коливань з періодом nT – n точок), а при виникненні квазіперіодичних коливань переріз Пуанкаре є замкнутою кривою. Тому, якщо в результаті дослідження системи, отримані перерізи, які відрізняються від кінцевого числа точок і замкнутої кривої, при цьому переріз Пуанкаре не виходить за межі певної області систему можна вважати хаотичною. Для систем з періодичною зовнішньою дією крок Т доцільно обирати рівним періоду зовнішньої дії.