Лекція 7

Після виникнення збурення в системі починається перехідний процес у_пер (t), після завершення якого система перейде в усталений режим роботи, рис. 1.

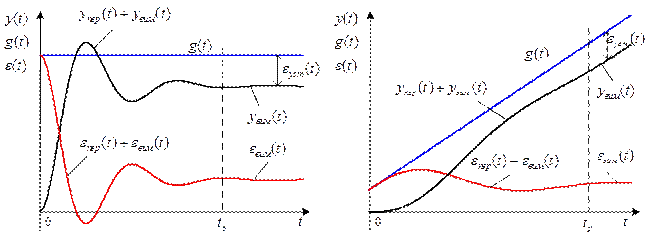
Рис. 1. Графіки перехідних процесів

Як видно з рис. 1 з форми усталеного режиму у_вим(t) визначається точність системи керування. При цьому усталена похибка ε_уст(t) системи дорівнює:

, (1)

де g(t) – задаюча дія.

Повне значення помилки визначається аналогічно:

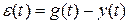. (2)

Точність системи задається і визначається в усталеному режимі роботи системи керування. Повне значення помилки ε(t), що визначає точність роботи системи, представляє собою суму перехідної і вимушеної складової помилки:

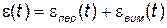. (3)

Після затухання перехідної складової похибки , тобто після закінчення перехідного процесу, точність роботи системи визначається вимушеною складовою помилки 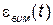. Якщо відома передавальна характеристика для помилки за задавальною дією , то зображення помилки має такий вид:

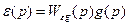, (4)

Іноді задача підвищення точності систем керування може бути вирішена достатньо просто – шляхом збільшення коефіцієнту підсилення розімкненої системи. Але частіше доводиться вводити додаткові ланки в структуру регулятора або взагалі використовувати інший принцип керування. При вирішенні задачі підвищення точності системи керування необхідно враховувати також стабільність характеристик інших вузлів системи керування:

- стабільності напруги опорного джерела;

- коливання частоти задавального генератора;

- розрядності АЦП;

- інерційності контуру керування.

Загальними методами підвищення точності систем керування є:

1. Збільшення коефіцієнту підсилення розімкненого ланцюга.

2. Збільшення порядку астатизму.

3. Застосування регулювання за похідними.

4. Використання комбінованого керування.

5. Введення неодиничних зворотних зв’язків.

Підвищення точності за рахунок збільшення коефіцієнту підсилення

Розглянемо систему керування другого порядку, передавальна характеристика якої показана на рис. 1.

Рис. 1.

Помилка її керування рівна:

. (5)

Зрозуміло, що помилка зменшуватиметься при збільшенні коефіцієнту підсилення К. Обмеженням на величину коефіцієнта К накладає запас стійкості і погіршення динамічних показників системи, рис. 2.

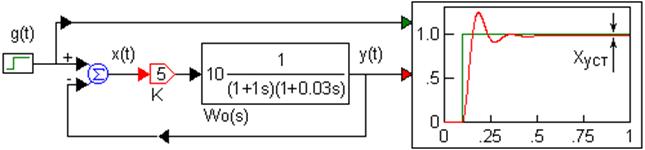
Рис. 2. Ефект від збільшення коефіцієнту підсилення

Підвищення точності за рахунок збільшення порядку астатизму

Підвищення порядку астатизму використовується для усунення помилок в усталених режимах системи, для чого використовують інтегруючі ланки. Однак інтегруюча ланка вносить запізнення по фазі на 90º. Тому послідовне включення навіть двох ланок призводить до нестійкої роботи, рис. 3.

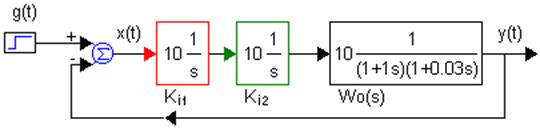
Рис. 3. Фазова та амплітудна передавальні характеристики системи

без астатизму (синій колір) і з астатизмом першого (червоний) та другого порядків (зелений)

Це обмеження усувається при використанні ізодромних пристроїв:

. (6)

Якісний вид передавальних характеристики ізодромних пристроїв показано на рис. 4.

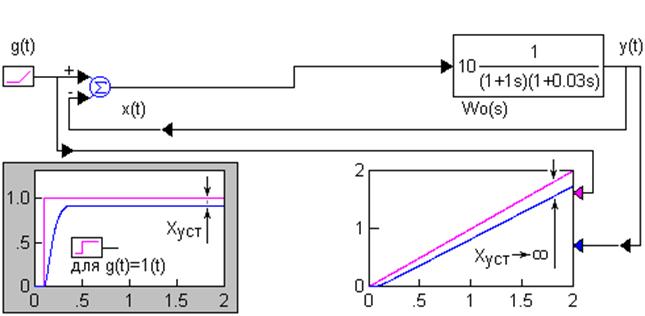
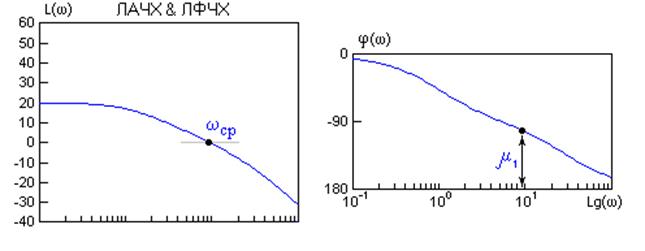
а) передавальні характеристики системи без ізодромних пристроїв

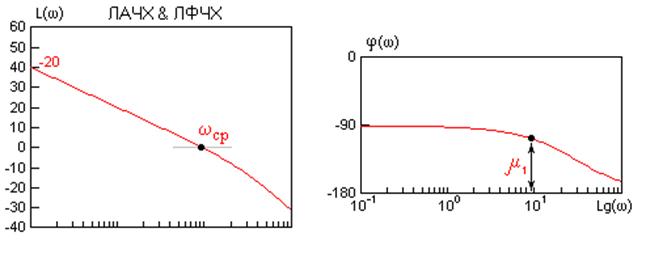
б) передавальні характеристики системи з одним ізодромним пристроєм

б) передавальні характеристики системи з двома ізодромними пристроями

Рис. 4.

По ЛАЧХ і ЛФЧХ видно, що постійну часу ізодромних ланок Т_і потрібно обрати значно більшою, ніж найбільша стала часу системи, щоб фазовий зсув ізодромних ланок не був суттєвим в області частоти зрізу і не впливав на стійкість системи. Ця особливість ізодромних пристроїв затягує перехідні процеси в системі і погіршує її динамічні властивості.

Підвищення точності застосуванням регулювання по похідним помилки

Причини підвищення точності при застосуванні регулювання по похідним помилки:

- система відпрацьовує помилки не лише по абсолютному значенню, але і за її приростом;

- підвищується запас стійкості по фазі і можна збільшити загальний коефіцієнт підсилення.

Рис. 5. Характеристики систем з регулюванням по похідній

Підвищення точності при застосуванні комбінованого керування

1. Застосування компенсувального пристрою по задавальній дії.

Рис. 6. Система с компенсувальним пристроєм по задавальній дії

Залежність зображення вихідного сигналу від жадаючої дії:

. (7)

Умова повної інваріантності:

. (8)

Для зменшення перехідних процесів в системі з компенсувальним пристроєм також можна застосувати диференційні ланки, рис. 7.

Рис. 7. Перехідні процеси в інваріантній системі

2. Застосування компенсувального пристрою після регулятора. На рис. 8 показана структура системи і перетвореної схеми, отриманої для виведення передавальної характеристики.

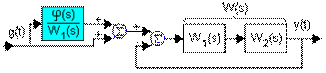
Рис. 8. Система з компенсуючим пристроєм після регулятора

Залежність зображення вихідного сигналу від жадаючої дії:

. (9)

Умова інваріантності:

. (10)

3. Застосування компенсуючого пристрою по збуренню, рис. 9.

Рис. 9. Система з компенсувальним пристроєм по збуренню

Передавальна характеристика системи:

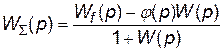. (11)

Умова інваріантності:

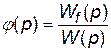. (12)

Перевага компенсувальних пристроїв:

- не змінюють коренів характеристичного рівняння системи.

Недоліки:

- необхідне точне налаштування коефіцієнтів передавальної функції φ(р);

- при зміні параметрів W(p) з’являються помилки.

Підвищення точності системи за рахунок застосування неодиничних зворотних зв’язків

Введення неодиничних зворотних зв’язків дозволяє зменшити помилку, викликану задавленою дією, рис. 10.

Рис. 10. Система з не одичним зворотним зв’язком

Передавальна характеристика системи:

. (13)

Умова інваріантності:

. (14)

Лекція 7