
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лінеаризація моделі
Для розрахунку стійкості в малому рівняння (1) і (2), що описують процеси в силовій частині і системі керування, лінеаризують. При цьому розглядаються нескінченно малі відхилення змінних стану dX(mT)=Xξ(mT) відносно початкових умов X(mT). Розглянемо процес зміни значень змінних стану для t>mT. Значення змінних стану в довільний момент часу є функцією початкових умов і часу: Х(t) = f (X(mT),t). При розрахунку диференціалу змінних стану необхідно знайти похідні по кожній змінній:
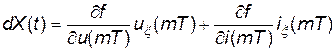 ,
,
або
 . (3)
. (3)
Лінеаризація рівнянь здійснюється за початковими умовами. Лінеаризація системи (1) є такою:
 . (4)
. (4)
Для системи керування, з врахуванням, що напруги ur і ug не залежать від змінних стану, отримаємо:


або
 . (5)
. (5)
Зважаючи на (5):
 , (6)
, (6)
де  .
.
Похідна  , згідно з рис. 1, містить δ-функцію, тобто
, згідно з рис. 1, містить δ-функцію, тобто  = δ(uzw). Для опису часової залежності δ(uzw) розглянемо повну залежність s(uzw(t)). Оскільки функція s(uzw(t)) є функцією часу, рис. 2, то її похідна за часом описується наступним виразом:
= δ(uzw). Для опису часової залежності δ(uzw) розглянемо повну залежність s(uzw(t)). Оскільки функція s(uzw(t)) є функцією часу, рис. 2, то її похідна за часом описується наступним виразом:
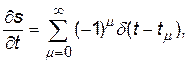 (7)
(7)
де  - функція Дірака.
- функція Дірака.

Рис. 2. Залежність функції s(uzw(t))
Похідна функції перемикання розраховується як складна функція:
 , (8)
, (8)
при чому  . Для зручності похідна
. Для зручності похідна  позначається
позначається  . Оскільки ліві частини виразів (7) і (8) рівні, прирівняємо праві частини між собою:
. Оскільки ліві частини виразів (7) і (8) рівні, прирівняємо праві частини між собою:
 . (9)
. (9)
З цього виразу виражаємо  :
:
 . (10)
. (10)
Зважаючи на те, що похідна  >0 у випадку, коли
>0 у випадку, коли  >0, можна записати:
>0, можна записати:
 . (11)
. (11)
Якщо використати наступну властивість δ-функції:  , вираз (11) можна записати наступним чином:
, вираз (11) можна записати наступним чином:
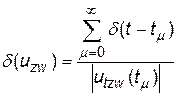 , (12)
, (12)
де  - похідна функції uzw(tμ) в точці tμ.
- похідна функції uzw(tμ) в точці tμ.
Так як система керування спочатку фіксує значення сигналу керування, а потім відбувається комутація, то значення функції обчислюється ліворуч від точки комутації tμ. Таким чином:
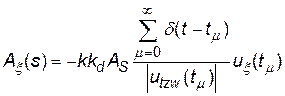 , (13)
, (13)
де  .
.
Аналогічно:
 . (14)
. (14)
Підставляючи отримані вирази в лінеаризоване рівняння (4), отримаємо:
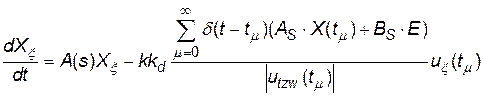 . (15)
. (15)
При цьому 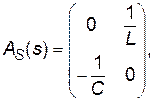
 .
.
Дата добавления: 2014-12-03; просмотров: 414; Мы поможем в написании вашей работы!; Нарушение авторских прав |