Лекція № 9. Методи забезпечення інваріантності замкнених систем

Модель триплечового БПЧ показана на рис. 1.

Рис. 1. Модель триплечового БПЧ

В якості вхідних змінних приймаються напруги u_ap, u_bp, u_cp, а в якості вихідних - u_an, u_bn, u_cn. Фазні напруги навантаження виражаються формулами:

;

; (1)

.

Матриця переходу для БПЧ має наступний вигляд:

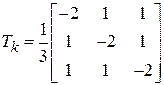. (2)

Як було показано у попередній лекції простір вихідних змінних триплечового перетворювача представляється на площині у системі з трьох вихідних змінних, незалежними з яких є дві з них. Тому таку систему часто представляють за допомогою двох змінних – проекцій вихідних напруг на дві ортогональні осі – d і q. Система рівнянь для переходу в dq площину має наступний вид:

. (3)

Формула для перетворення вхідних напруг перетворювача в ортогональні складові dq-простору є добутком матриць Т_к і Т_dq:

. (4)

Для побудови інваріантного для деяких зовнішніх збурень керування нелінійна математична модель двигуна лінеаризується:

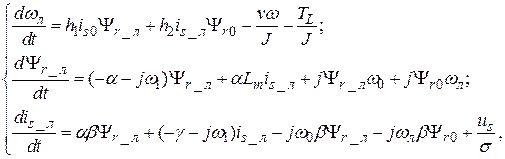(5)

h_1, h₂ – коефіцієнти лінеаризації.

До лінеаризованих змінних у системі (5) додано індекс – _л. Значення змінних в околі робочої точки позначено індексом – ₀.

Після приведення подібних доданків з системи (5) отримано такий вираз.

Для зручності індекси лінеаризації не позначено. В матричному вигляді система описується наступним виразом:

.

На рис. 2 наведено структурну схему варіанту замкненої системи на основі системи (6).

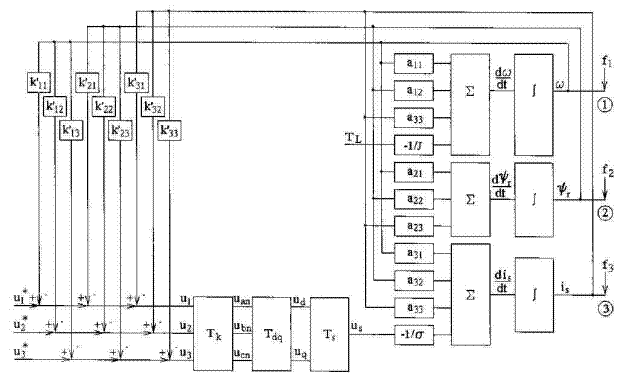
Рис. 2. Структурна схема моделі замкненої системи на асинхронного двигуна

До схеми входять блоки, які містять коефіцієнти матриці А, суматори і інтегратори. Вихідні змінні двигуна i_s, ω, Ψ формуються на виході інтеграторів, де на них діють зовнішні збурення f₁, f₂, f₃. У системі введені зворотні зв’язки k_ij. Вектор вхідних напруг u_s на основі геометричного підходу описується складовими напругами u₁, u₂, u₃, які знаходяться відніманням від заданих значень u₁^*, u₂^*, u₃^* сигналів зворотного зв’язку:

Для виведення залежності вектору вхідних змінних u_s від заданих впливів u₁^*, u₂^*, u₃^*, вектор вихідних напруг виражається через вхідні:

dq-складові вектора напруг статора

звідки

Рівняння (7) дозволяють виразити вектор напруги статора двигуна (вихідної напруги БПЧ) через напруги зворотних зв’язків введених до системи:

Рівняння (8) є загальним і справедливе для системи, рис. 2, в якій наявні всі зворотні зв’язки. В деяких випадках достатнім є введення зворотних зв’язків лише по одному параметру двигуна. Тоді рівняння (8) спроститься до виду:

Нехай f₁, f₂, f₃ – збурення, що впливають на зміни частоти обертання ротору ω, потоку ротора Ψ, струму статора i_s. Тоді модель рис. 2 відносно вузлів 1, 2, 3 можна описати у матричній формі:

DX = F,

де D – матриця 3х3, Х – вектор змінних, F – вектор збурень.

Коефіцієнти матриці D розраховуються за структурною схемою рис. 2:

В якості збурення, що впливає на перший вузол системи може бути момент навантаження Т_L. З врахуванням цього типу збурення матриця D має такий вигляд:

Для забезпечення інваріантності швидкості обертання відносно моменту навантаження T_L, необхідне виконання умови:

D₁₁ = 0,

тобто

З розв’язку рівняння (9) знаходиться передавальна характеристика зворотного зв’язку k₂₂:

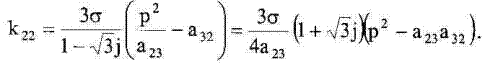
Підставивши замість коефіцієнтів a_ij параметри моделі двигуна отримаємо:

Ланка зворотного зв’язку, що реалізує задану передавальну характеристику, показана на рис. 3.

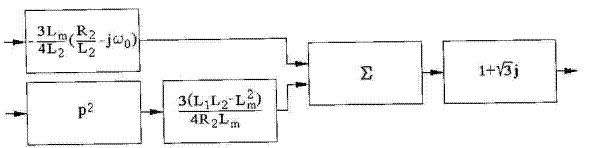
Рис. 3. Ланка зворотного зв’язку

Для асинхронного двигуна з наступними параметрами: опори обмоток статора R₁ = 4.7 Ом і ротора R₂ = 5.3 Ом, індуктивності обмоток статора L₁ = 0.185 Гн і ротора L₂ = 0.185 Гн, індуктивності контуру намагнічування L_m = 0.18 Гн при ω₀ = 0 коефіцієнт k₂₂ дорівнює:

.