Основні засади теорії інваріантності

Теорія інваріантності є розділом теорії автоматичного регулювання, яка розглядає проблеми повної або часткової компенсації впливу збурень на системи автоматичного регулювання і ідеального відтворення задаючих сигналів.

Зменшення величини помилки можна досягти за рахунок збільшення коефіцієнту підсилення, введенням коректуючих пристроїв, збільшенням астатизму системи. Однак застосування вказаних методів пов’язане зі зменшенням запасу стійкості системи, тому при їх використанні повністю помилку усунути не вдається.

Лише за умов інваріантності системи відносно певного типу збурень вдається повністю усунути помилку, пов’язаною з її появою. Визначення умови інваріантності системи здійснюють за диференційними рівняннями системи автоматичного регулювання:

, (1)

де - диференційні оператори,

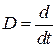- оператор диференціювання,

с_ij, r_ij, k_ij – постійні коефіцієнти,

х_і – змінні стану системи,

f – збурення.

Аналіз інваріантності змінної стану х₁ відносно збурення f здійснюють за рівнянням:

Δ·х₁ = А₁₁· f, (2)

де - головний визначник системи,

- алгебраїчне доповнення елемента а₁₁ матриці А.

З рівняння (2) випливає, що якщо алгебраїчне доповнення А₁₁ тотожно рівне нулю А₁₁ = 0, змінна стану х₁ інваріантна відносно збурення f.

Слід зазначити, що інваріантність системи забезпечується за рахунок ускладнення структури системи керування. Для забезпечення інваріантності по одній змінній, система керування повинна мати мінімум два канали регулювання. Розглянемо застосування теорії інваріантності для систем керування двигунів.