Методи аналізу процесів у перетворювачах

Метод припасовування

Одним з найбільш загальних підходів аналізу, який дозволяє досліджувати процеси у перетворювачі будь-якої структури, схема заміщення якого складається з лінійних елементів, ідеальних моделей ключів і кусково-лінійних моделей інших елементів перетворювача є метод припасовування. Суть методу припасовування полягає у послідовному розрахунку процесів, починаючи з першого інтервалу роботи. При цьому значення напруг на ємностях і струмів у індуктивностях на початку кожного наступного періода (початкові умови) є значеннями цих же струмів і напруг в кінці попереднього інтервалу роботи перетворювача. При цьому для розрахунку процесів на інтервалах застосовуються методи, призначені для лінійних ланцюгів. Практично для цього використовуються чисельні або чисельно-аналітичні методи розрахунку, оскільки використання аналітичних методів обмежується ланцюгами не вище другого порядку.

Чисельні методи

Найчастіше в якості метода розрахунку перехідного процесу на інтервалах використовується метод змінних стану. Цей метод базується на матричній формі запису диференційних рівнянь системи відносно змінних стану. Змінними стану є струми у індуктивностях і напруги на ємностях. Для ланцюга порядку n, n – кількість реактивних елементів ланцюга, до якого підключено m джерел енергії, система диференційних рівнянь у матричній формі має наступний вид:

а) понижуючий перетворювач; б) підвищуючий перетворювач; в) інвертуючий перетворювач; г) мостовий інвертор

Рис. 1. Схеми заміщення перетворювачів

а) понижуючий перетворювач; б) мостовий інвертор

Рис. 2. Спрощені схеми заміщення перетворювачів

, (1)

де Х – вектор-стовпець змінних стану,

А – матриця розмірності n x n, елементи якої визначаються топологією і параметрами елементів електричного ланцюга,

В – матриця розмірності m x n, яка визначає вклад зовнішніх джерел енергії (зовнішньої дії) на баланс струмів і напруг ланцюга,

V – вектор-стовпець зовнішньої дії.

Для вирішення системи рівнянь (1) використовують методи чисельного інтегрування.

Правила формування матриць А і В розглянемо на прикладі лінійної схеми заміщення понижуючого ШІП, рис. 3.

Рис. 3. Лінійна схема заміщення понижуючого ШІП

Матриця А описує вплив змінних стану на перехідний процес. Матриця А ланцюга рис. 3 має розмірність 2х2. Для розрахунку значень її елементів спочатку необхідно пронумерувати змінні стану. Нехай струм у індуктивності L є першою змінною стану, напруга на ємності С – другою змінною стану. Значення її елементів задаються такими виразами:

, (2)

де А₁₁ – вхідний опір резистивної частини ланцюга відносно виводів індуктивності L при закорочуванні ємності та джерела напруги Е. Для ланцюга рис. 3, А₁₁ = R. Знак перед коефіцієнтом залежить від того чи співпадає полярність струму і напруги з вибраними до розрахунку. В нашому випадку при вказаній полярності напруги на індуктивності струм через неї має протікати в протилежному напрямі, ніж вибраний напрям струму, тому А₁₁ = -R.

А₁₂ – коефіцієнт передавання напруги від ємності С до індуктивності L, за умови розривання індуктивності і закорочуванні джерела напруги Е. А₁₂ = -1.

А₂₁ – коефіцієнт передавання струму від індуктивності L до ємності С, за умови закорочування ємності і джерела напруги Е. А₂₁ = 1.

А₂₂ – вхідна провідність резистивної частини ланцюга відносно виводів ємності С при розриванні індуктивності і закорочуванні джерела напруги Е. А₂₂ = -1/R_H.

За результатами розрахунків матриця А має наступний вид:

. (3)

Матриця В має розмірність 1х2:

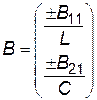, (4)

де В₁₁ – коефіцієнт передавання напруги від джерела Е до індуктивності L, якщо і_L = 0 і ємність С закорочена. В₁₁ = 1.

В₂₁ – провідність передавання від джерела напруги Е до гілки з ємністю С за умови розривання індуктивності і закорочуванні ємності. В₂₁ = 0.

Система диференційних рівнянь, сформована методом змінних стану, з урахуванням розрахованих значень матриць А і В:

. (5)

Розглянемо ланцюг, що зображений на рис. 4.

Рис. 4. Досліджуваний ланцюг

Система рівнянь, сформована методом змінних стану для ланцюга рис. 4:

, (6)

де , , ,

, , ,

, , .

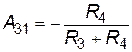Систему диференційних рівнянь типу (6) необхідно скласти для кожної лінійної схеми заміщення перетворювача. Після цього проводиться дискретизація отриманих рівнянь за допомогою обраного метода чисельного інтегрування. Крок інтегрування Δt_і обирається з умов необхідної точності розрахунків. Як правило Δt_і << T, тому використання чисельних методів призводить до значного збільшення проміжних точок, в яких розраховується перехідний процес.