
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Математична модель БПЧ
При розробці інваріантних систем однією з основних проблем є побудова максимальної кількості каналів керування. Кількість каналів залежить від вибору системи змінних перетворювача. Як правило, для цього використовується геометричний підхід. Розглянемо застосування геометричного підходу до автономного інвертора напруги, рис. 3.

Рис. 3. Інвертор напруги
Напруга кожної стійки інвертора може приймати два значення: 0 або Ud. Вихідна напруга інвертора визначається як
Uab = Uag – Ubg. (6)
Зважаючи на це, інвертор може перебувати у чотирьох станах, які описані у табл.1.
Таблиця 1. Можливі стани інвертора напруги
| Sa | Sb | Uag | Ubg | Uab | № вектора |
| Ud | -Ud | ||||
| Ud | +Ud | ||||
| Ud | Ud |
Два плеча інвертора складають систему двома ступенями свободи, тому що кожним плечем можна керувати незалежно. Це відповідає моделі, що має дві ортогональні вісі, вздовж яких кожна плечова напруга змінюється зі значення 0 до +Ud. Вихідна напруга отримується за допомогою проекції напруг плечей інвертора на лінію, перпендикулярну вектору [1 1]T у просторі плечових напруг. Цю проекцію зображену на рис. 4.

Рис. 4. Простори плечових і вихідних напруг інвертора
Чотири кути квадрату плечових напруг представляють чотири стани переключення інвертора. Проекцію переходу від плечових напруг у простір вихідних напруг можна представити за допомогою матриці переходу, де плечові напруги перетворюються у вихідну напругу і змінну-фіксатор, позначену як U0.
 . (7)
. (7)
За допомогою фіксатора U0 враховується втрата одного ступеня свободи при переході від плечових напруг до вихідної напруги.
При аналізі трифазного інвертора, рис. 5, видно що він може знаходитись у восьми станах. Плечові напруги утворюються систему з трьома ступенями свободи, тобто тривимірний простір, рис. 6.

Рис. 5. Трифазний інвертор
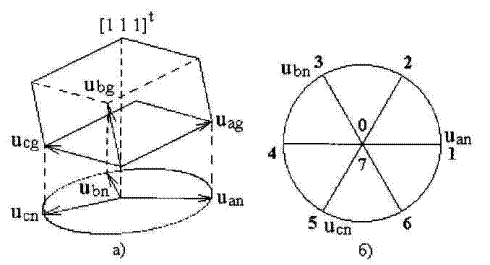
а) простори плечових і вихідних напруг; б) основні вектори напруг в просторі вихідних напруг
Рис. 6. Вектори напруг трифазного інвертора
Згідно з рис. 6 вихідні напруги інвертора є проекцією простору вхідних напруг на площину перпендикулярну вектору [1 1 1]T. Вісім кутів куба представляють вісім станів інвертора. Простір вихідних напруг двовимірний, отже серед трьох вихідних напруг незалежними будуть лише дві. Матриця переходу трифазного інвертора:
 . (8)
. (8)
Застосуємо геометричний підхід до БПЧ:

Рис. 7. Моделі БПЧ

Рис. 8. Простори вхідних і вихідних змінних БПЧ
n-плечовий перетворювач описується n вхідними змінними і (n-1) вихідними змінними. Перехід від вхідних до вихідних змінних здійснюється за формулою:
uвих = ТК·uвх. (9)
При використанні геометричного підходу необхідно враховувати особливості роботи БПЧ у порівнянні з автономними інверторами. Першою особливістю є те, що на вході і на виході БПЧ формується змінна напруга, при цьому частоти цих напруг відрізняються. Тому у БПЧ в якості напруг на розімкнених ключах доцільно використовувати лінійні напруги в схемах без нульового дроту і фазні – у схемах з нульовим дротом.
Другою особливістю є те, що до однієї фази навантаження може бути підключена будь-яка фаза мережі. Для спрощення моделі цього явища пропонується підхід, зображений на рис. 9.

а) схема плеча; б) модель плеча
Рис. 9. Модель плеча БПЧ
Ключем S1.f моделі відповідають три різних ключі схеми залежно від інтервалу часу, який задається змінною f. Вузол р моделі може бути з’єднаний з однією з фаз мережі: В або С. Між вузлом р і ключем S1.f під’єднано джерело напруги, яке має різні значення в залежності від змінної f. Змінна f може приймати наступні значення:

В якості вхідних змінних БПЧ приймаються напруги між точкою підключення фаз навантаження до плечей силових ключів і точкою р uap. В якості вихідних змінних використовуються фазні напруги навантаження БПЧ.
Дата добавления: 2014-12-03; просмотров: 417; Мы поможем в написании вашей работы!; Нарушение авторских прав |