
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Поняття міркування, правильні та неправильні міркування. Перевірка правильності міркувань з допомогою кругів Л.Ейлера.
4. У своїй практичній діяльності людина спирається на закони природи та суспільства. Знання про них вона одержує, в основному, трьома способами: 1) спостерігаючи явища та речі в природних умовах і накопичуючи завдяки цьому відомості про оточуючий світ; 2) проводячи експерименти у штучностворених нею умовах; 3) міркуючи та одержуючи в результаті цих міркувань нові знання із відомих раніше. Вказані три способи є джерелами науки. Співвідношення трьох основних джерел в різних науках різне. У зв’язку з цим прийнято розрізняти описові, дослідні (експериментальні або емпіричні) та дедуктивні науки. До описових наук відносять комплекс географічних наук, зоологію, до експериментальних – фізику, хімію, до дедуктивних – математику, логіку.
Зазначимо, що такий поділ на вказані види наук досить відносний, бо в ході їх розвитку співвідношення між спостереженнями, експериментом і міркуваннями змінюється. У наш час спостерігається проникнення логічних і математичних методів в розділи наук, які вважалися у недалекому минулому описовими, наприклад, в біологію, економіку, лінгвістику тощо. У дедуктивних науках основним методом досліджень вважається виведення наслідків із невеликої кількості вихідних положень. Вони, як правило, є результатом досвіду та спостережень. Зміст і форма дедуктивних наук характеризується, головним чином, тим багатством наслідків, які можна та які одержані за допомогою міркувань.
Будь-яке міркування складається із ланцюжка висловлень, які випливають один з одного за певними правилами. Вміння міркувати, правильно обґрунтовувати свої висновки необхідне людині будь-якої професії. Людина вчиться міркувати, починаючи з того моменту, коли вона починає говорити. Разом з тим, цілеспрямоване навчання логіці міркувань починається в школі. Вже при вивченні курсу математики початкових класів учні розвивають уміння аналізувати, порівнювати, класифікувати, обґрунтовувати найпростіші твердження тощо. Саме тому вчитель початкових класів повинен бути обізнаним з наукою про закони і форми мислення, про загальні схеми міркувань. Основні типи суджень і умовиводів, що лежать в основі міркувань, розглядаються в класичній логіці, засновником якої вважається філософ стародавньої Греції Аристотель (384-422 рр. до н. е.).
В основі обґрунтування та доведення лежать міркування, під якими розуміють логічну операцію, в результаті якої із одного або декількох взаємопов’язаних за змістом речень одержують речення, що містить нове по відношенню до вихідних знання. Якщо проаналізувати структуру міркування, то можна помітити, що будь-яке з них складається із умови (або посилок) та висновку. Розглянемо міркування: якщо число просте, то воно має два дільники. В ньому посилкою є “якщо число просте”, а висновком - “то воно має два дільники”. Всі міркування можна поділити на дві великі групи: 1) дедуктивні міркування, в яких між посилкою і висновком має місце відношення слідування; 2) індуктивні міркування, в яких на підставі того, що деякі об’єкти множини мають певні властивості, робиться висновок про те, що цю властивість мають всі об’єкти цієї множини. Прикладом дедуктивного міркування може бути таке “якщо число кратне 8, то воно кратне 2“, а індуктивного - “2 кратне 2, бо закінчується 2, 4 кратне 4 бо закінчується 4. Отже, всі числа, які закінчуються на 2 і 4 діляться на 2”. Якщо дедуктивні міркування будуються за правилами логіки, то ми повинні з правильної посилки одержати правильний висновок. Для індуктивних міркувань цього сказати не можна.
Процес мислення має надзвичайно складний характер і відбувається у переплетінні тисячоліттями відшліфованих строгих форм утворення умовиводів, поки що не вивчених інтуїтивних уявлень і творчих актів, певних емоційних сторін діяльності вищої нервової системи людини тощо. Проте, ще стародавні мислителі відзначали, що істотна частина наших умовиводів робиться за певними стандартними схемами, які не залежать від того конкретного матеріалу, що ми ними оперуємо. Внаслідок вивчення цього процесу людського мислення виникла наука, яка одержала назву «формальна логіка». Вона займається вивченням способів утворення правильних висновків, виходячи з певних зв’язків між формою, структурою посилок або умов, а не з їхнього конкретного змісту.
Розглянемо кілька міркувань та з’ясуємо, як вони побудовані: 1) «якщо всі птахи - тварини і всі горобці - птахи, то всі горобці - тварини»; 2) «якщо всі птахи – тварини і всі квіти – птахи, то всі квіти - тварини»; 3) «якщо деякі французи – блондини і дехто з курців – французи, то деякі курці - блондини»; 4) «якщо деякі опуклі фігури – круги і деякі опуклі фігури – многокутники, то деякі многокутники - круги». Кожне з наведених міркувань складається з трьох висловлень. У перших двох прикладах у першому висловленні стверджується, що всі предмети деякого класу мають деяку властивість, яка є істотною для всіх предметів цього класу, а у другому висловленні стверджується, що всі предмети цього ж класу є частковим випадком більш загального поняття. У третьому та четвертому прикладах у першому висловлення стверджується, що деякі предмети мають певну властивість, яка є істотною для всіх предметів цього класу, а в другому висловленні цих прикладів стверджується, що деякі предмети є частковим випадком більш загального поняття. На цій основі робиться висновок про те, що відзначена властивість належить або всім, або деяким поняттям. Загальну форму цього міркування для перших двох прикладів можна представити так: «якщо всі предмети класу А мають властивість α і обсяг класу В є частиною обсягу класу А, то всі об’єкти класу В мають властивість α». Загальну форму цього міркування для двох останніх прикладів можна представити так: «якщо деякі предмети класу А мають властивість α і обсяг класу В є частиною обсягу класу А, то деякі об’єкти класу В мають властивість α». Міркування такого вигляду називають силогізмами. Форма міркування вважається правильною, якщо при істинності вихідних тверджень, вона завжди приводить до правильних висновків. Цілком зрозуміло, що при хибності вихідних тверджень навіть за допомогою правильного за формою міркування, можна прийти до хибного висновку.
Якщо проаналізувати наведені приклади з точки зору їх істинності, то одержимо таке: 1) у першому прикладі з двох правильних висловлень ми одержуємо істинний висновок; 2) хибність висновку другого прикладу відбулася не від хибності схеми, а від хибності однієї з посилок; 3) у третьому прикладі, незважаючи на істинність всіх висловлень, ми одержуємо логічну помилку у висновку; 4) четвертий приклад є ілюстрацією до третього. Таким чином, логічні висновки повинні робитися за певною схемою, а правильними вважаються лише ті схеми, які з істинних посилок завжди приводять до істинних висновків.
В аристотелівській логіці розглядаються чотири види так званих категоричних судження: 1) загально стверджувальне судження – А=«Всі S суть P»; 2) загальнозаперечувальне судження – Е=«Всяке S не є P»; 3) частково стверджувальне судження – І=«Деякі S суть P»; 4) частковозаперечувальне судження – О=«Деякі S не суть P». Їх прийнято класифікувати, по-перше, «по якості»: А, І – стверджувальні судження; Е, О – заперечувальні судження; по-друге, «по кількості»: А, Е – загальні судження; І, О – часткові судження. Розглянемо всі чотири види суджень з точки зору теорії предикатів.
Для запису загально стверджувального судження А=«Всі S суть P» використаємо квантор загальності, предикати S(х) і P(х) та імплікацію предикатів S(х)→P(х). Тоді символічний запис цього судження буде мати вигляд ("хєХ)(S(х)→P(х)) та читатиметься так: «для всіх хєХ, якщо х має властивість S, то х має властивість Р». Прикладом таких тверджень є «всі риби - тварини», «всі люди - смертні», «всі квадрати – прямокутники» тощо.

 Для запису загальнозаперечувальне судження Е=«Всяке S не є P» використаємо квантор загальності, предикат S(х), заперечення предикату P(х) та імплікацію предикатів S(х)→P(х). Тоді символічний запис цього судження буде мати вигляд ("хєХ)(S(х)→P(х)) та читатиметься так: «для всіх хєХ, якщо х має властивість S, то х немає властивості Р». Прикладом таких тверджень є «всі риби не є птахами», «будь-які камені не є тваринами», «будь-які трикутники не є квадратами» тощо.
Для запису загальнозаперечувальне судження Е=«Всяке S не є P» використаємо квантор загальності, предикат S(х), заперечення предикату P(х) та імплікацію предикатів S(х)→P(х). Тоді символічний запис цього судження буде мати вигляд ("хєХ)(S(х)→P(х)) та читатиметься так: «для всіх хєХ, якщо х має властивість S, то х немає властивості Р». Прикладом таких тверджень є «всі риби не є птахами», «будь-які камені не є тваринами», «будь-які трикутники не є квадратами» тощо.
Для запису частково стверджувального судження І=«Деякі S суть P» використаємо квантор існування, предикати S(х) і P(х) та кон’юнкцію предикатів S(х)ÙP(х). Тоді символічний запис цього судження буде мати вигляд ($хєХ)(S(х)ÙP(х)) та читатиметься так: «існує таке хєХ, який має властивість S і також має властивість Р». Прикладом таких тверджень є «деякі люди палять», «деякі швейцарці говорять французькою», «деякі прості числа - парні» тощо.
 Для запису частковозаперечувального судження О=«Деякі S не суть P» використаємо квантор існування, предикат S(х), заперечення предикату P(х) та кон’юнкцію предикатів S(х)ÚP(х). Тоді символічний запис цього судження буде мати вигляд ($хєХ)(S(х)ÚP(х)) та читатиметься так: «існує таке хєХ, який має властивість S і також немає властивості Р». Прикладом таких тверджень є «деякі тварини не дихають легенями», «деякі гриби не їстівні», «деякі трикутники не рівнобедрені» тощо.
Для запису частковозаперечувального судження О=«Деякі S не суть P» використаємо квантор існування, предикат S(х), заперечення предикату P(х) та кон’юнкцію предикатів S(х)ÚP(х). Тоді символічний запис цього судження буде мати вигляд ($хєХ)(S(х)ÚP(х)) та читатиметься так: «існує таке хєХ, який має властивість S і також немає властивості Р». Прикладом таких тверджень є «деякі тварини не дихають легенями», «деякі гриби не їстівні», «деякі трикутники не рівнобедрені» тощо.

 На основі наведених суджень можна легко побачити деякі співвідношення між ними, які детально вивчалися в аристотелівській логіці. Наприклад, загальностверджувальне судження А і частковозаперечувальне судження О є запереченнями один одного. Аналогічно загальнозаперечувальне судження Е і частково стверджувальне судження І є запереченнями один одного. У традиційній логіці говорять, що загальностверджувальне судження А і частковозаперечувальне судження О (загальнозаперечувальне судження Е і частковостверджувальне судження І) знаходяться у відношенні протиріччя один до одного. Таким чином, аристотелівські силогізми являють собою схеми логічних виводів, які складаються з трьох суджень одного з названих чотирьох видів А, Е, І, О. Наведемо приклади силогізмів, які є досить поширеними (див. таблицю № 2.12.).
На основі наведених суджень можна легко побачити деякі співвідношення між ними, які детально вивчалися в аристотелівській логіці. Наприклад, загальностверджувальне судження А і частковозаперечувальне судження О є запереченнями один одного. Аналогічно загальнозаперечувальне судження Е і частково стверджувальне судження І є запереченнями один одного. У традиційній логіці говорять, що загальностверджувальне судження А і частковозаперечувальне судження О (загальнозаперечувальне судження Е і частковостверджувальне судження І) знаходяться у відношенні протиріччя один до одного. Таким чином, аристотелівські силогізми являють собою схеми логічних виводів, які складаються з трьох суджень одного з названих чотирьох видів А, Е, І, О. Наведемо приклади силогізмів, які є досить поширеними (див. таблицю № 2.12.).
Вважають, що в основі кожного дедуктивного міркування лежить певне правило виводу, серед яких ми виділимо такі:
1. Правило заключення, яке символічно запишеться так: ("хєХ)(А(х)®В(х)ÙА(a))®В(a). У цьому записі вираз ("хєХ)(А(х)®В(х)ÙА(a)) являє собою умову (посилку) міркування, яка представлена кон’юнкцією загальної та часткової посилки. У свою чергу вираз В(a) - це заключення або висновок міркування. Крім цього, А(a) - це часткова посилка, яка являє собою висловлення, одержане із предиката А(х) після підстановки замість змінної х конкретного значення, а В(a) – це висловлення, одержане із предиката В(х) після підстановки замість змінної х конкретного значення.
| Силогізм Barbara | Силогізм Darii | |
| «Всі М суть Р» «Всі S суть М» «Всі S суть Р» | «Всі М суть Р» «Деякі S суть М» «Деякі S суть Р» | «Деякі М суть Р» «Деякі S суть М» «Деякі S суть Р» |
| Риска після другого висловлення означає, що висновок є логічним наслідком посилок. | Риска після другого висловлення означає, що висновок є логічним наслідком посилок. | Риска після другого висловлення означає, що висновок є логічним наслідком посилок. |
| Всі висловлення цього силогізму є загальностверджувальними. | У даній схемі перша посилка є загальностверджувальним висловленням, а друга посилка і наслідок – частковостверджувальні. | У даній схемі всі три судження є частковостверджувальними. |
Таблиця № 2.12. Приклади силогізмів.
2. Правило заперечення, яке символічно запишеться так: ("хєХ)(А(х)®В(х)ÙВ(a))®А(a). У цьому записі вираз ("хєХ)(А(х)®В(х)ÙВ(a)) являє собою умову (посилку) міркування, яка представлена кон’юнкцією загальної та часткової посилки. У свою чергу вираз В(a) - це часткова посилка, яка являє собою висловлення, одержане із предиката В(х) після підстановки замість змінної х конкретного значення, а А(a) – це заключення або висновок міркування. Крім цього, А(a) - це висловлення, одержане із предиката А(х) після підстановки замість змінної х конкретного значення.
3. Правило силогізму, яке символічно записується так: ("хєХ)((А(х)→В(х)ÙВ(х)→С(х))→(А(х)→С(х))). Це правило виводу складається із двох загальних посилок ("хєХ)((А(х)→В(х))Ù(В(х)→С(х))), кон’юнкція яких задає нам умову міркування. Імплікація А(х)→С(х) є загальним висновком міркування.
Якщо множини істинності предикатів А(х), В(х) і С(х) зображати кругами Ейлера, то правильність міркувань можна перевірити за допомогою діаграм Ейлера-Венна. Для представлених у таблиці № 2.12 силогізмів будемо мати такі діаграми Ейлера-Венна (див. діаграми №№ 2.8-2.10.).
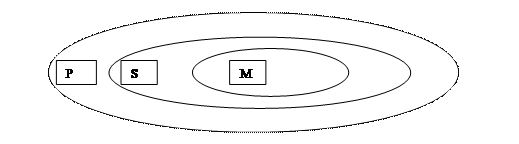
Діаграма № 2.8. Перевірка правильності силогізму Barbara за допомогою кругів Ейлера.
Вправа: перевірити правильність міркування ((А(х)→В(х))Ù(В(х)→С(х)))→(А(х)→С(х)), використовуючи круги Ейлера, якщо А(х): “натуральне число х кратне 16”, В(х): “натуральне число х кратне 8”, С(х): “натуральне число х кратне 4”.
Розв’язання:
Позначимо через А множину чисел, кратних 16, через В – множину чисел, кратних 8, і через С множину чисел, кратних 4. Тоді відношення між цими множинами за допомогою кругів Ейлера зобразиться так (див. діаграму № 2.11.).
Із наведеної діаграми видно: із того, що число х кратне 16 випливає, що число х кратне 8, а із того, що число х кратне 8 випливає, що воно кратне 4. Таким чином, використовуючи правило силогізму, ми також можемо переконатися у правильності вказаного міркування.

Діаграма № 2.9. Перевірка правильності силогізму Darii за допомогою кругів Ейлера.

Діаграма № 2.10. Перевірка правильності силогізму, який містить частково стверджувальні судження за допомогою кругів Ейлера.
 |
Діаграма № 2.11. Перевірка правильності міркувань за допомогою кругів Ейлера.
5*. Алгоритми. Основні властивості алгоритмів. Приклади алгоритмів, що використовуються в курсі математики початкової школи.
5*. Поняття алгоритму зустрічається як в математиці, так і в повсякденному житті. Точне визначення алгоритму в математиці не в усьому співпадає з інтуїтивним розумінням цього поняття в практичній діяльності людей. Термін алгоритм увійшов у активний словниковий запас людей завдяки значному застосуванню електронно–обчислювальної техніки в сучасному виробництві. Поняття алгоритму є одним із основних понять математики та інформатики. Ще задовго до використання інформатики в математиці застосовувалися різні алгоритми (або алгорифми). Зокрема, алгоритм письмового додавання, віднімання, множення, ділення, розкладу числа на прості множники, алгоритм Евкліда для знаходження НСД тощо.
Під алгоритмом розуміють точні вказівки щодо виконання у певному порядку деякої серії операцій для розв’язування задач певного типу. Наприклад: для рівняння ах=b маємо: 1. Якщо а≠0, то х=b:а. 2. Якщо а=0 і b≠0, то рівняння розв’язку немає. 3. Якщо а=b=0, то рівняння 0х=0 має безліч розв’язків, тобто х - будь-яке дійсне число.
Застосування алгоритму через скінченне число кроків приводить до розв’язання кожної задачі даного типу. Спільним для всіх алгоритмів є його характерні ознаки, до яких відносимо:
- повну визначеність алгоритму, тобто алгоритм повинен привести до результату;
- масовість алгоритму, тобто він повинен мати можливість застосуватись до множини випадків.
Алгоритми, за якими розв’язування поставлених задач зводиться до чотирьох арифметичних дій, називають числовими алгоритмами.
У теорії алгоритмів виділяють такі основні їх властивості:
1. Визначеність алгоритму, тобто алгоритм повинен бути записаним так, щоб не можна було неоднозначно тлумачити його вказівки.
2. Масовість алгоритму, тобто застосовність алгоритму до всіх задач одного типу.
3. Результативність алгоритму, тобто алгоритм повинен бути таким, щоб через певне число кроків, діючи за вказівками алгоритму, можна було б одержати розв’язок потрібної задачі даного типу.
4. Формальність алгоритму, тобто алгоритм повинен бути таким, щоб діючи за його вказівками, можна було б правильно виконати весь алгоритм.
Із курсу інформатики відомо, що існують такі способи описання алгоритму: а) словесний; б) табличний; в) графічний. Коли описують алгоритм, то ставлять певні вимоги, серед яких ми виділимо: точність, лаконічність, зрозумілість. Із курсу інформатики відомі декілька видів алгоритмів, серед яких ми виділимо: 1) лінійні алгоритми; 2) алгоритми з розгалуженнями; 3) циклічні алгоритми.
Означення: алгоритм називається лінійним, якщо в ньому дії виконуються послідовно одна за одною.
Означення: алгоритмом із розгалуженням називається алгоритм, в якому послідовність виконання операцій залежить від певних умов.
Означення: циклічним називається алгоритм, в якому група вказівок повторюється декілька разів.
В інформатиці сукупність засобів і правил запису алгоритмів називають алгоритмічною мовою.
Означення: програмою називають алгоритм, записаний на зрозумілій машині мові.
Означення: програмою називають послідовність команд, які повністю описують певний обчислювальний процес. Кожна команда описує певну частину обчислювального процесу.
Процес підготовки математичної задачі для її розв’язування на ЕОМ після вибору числового методу розв’язування називають програмуванням. В інформатиці виділяють такі етапи програмування: а) побудова алгоритму; б) розміщення в запам’ятовуючих пристроях машини вихідних даних, команд, допоміжних чисел, а також проміжних і кінцевих результатів; в) складання команд; г) перевірка і уточнення команд або програми.
Як в повсякденному житті, так і в математиці зустрічається дуже багато алгоритмів. Алгоритми зустрічаються вже в курсі математики початкової школи. Як правило, термін “алгоритми” для запам’ятовування молодшими школярами не вводиться. До алгоритмів, з якими зустрічаються неявно учні початкових класів в курсі математики можна віднести такі: 1) найрізноманітніші алгоритми усних та письмових обчислень; 2) алгоритми побудови геометричних фігур; 3) алгоритми розв’язування деяких типів задач; 4) алгоритми обчислення числових значень виразів із змінною при заданих значеннях букви. Досить часто вказані алгоритми даються учням у вигляді вказівок, які одержали назву алгоритмічних приписів. Наприклад, алгоритм множення двоцифрового числа на одноцифрове матиме такий вигляд: 1. Розклади перший множник на суму розрядних доданків: 23=20+3. 2. Помнож перший доданок на 4. 3. Помнож другий доданок на 4. 4. До 2 додай 3. 5. Запиши результат.
Алгоритм письмового ділення багатоцифрового числа на одноцифрове матиме такий вигляд: 1. Утвори перше неповне ділене. 2. Визнач кількість цифр у частці. 3. Поділи перше неповне ділене на дільник. 4. Запиши першу цифру частки. 5. Перевір першу цифру частки. 6. Перевір, чи правильно знайшли першу цифру частки. 7. Утвори друге неповне ділене. 8. Знайди другу цифру частки. 9. Перевір другу цифру частки. 10. Перевір, чи правильно знайдено другу цифру частки. 11. Утвори третє неповне ділене. 12. Знайди третю цифру частки. 13. Перевір третю цифру частки. 14. Закінчи обчислення.
Запитання для самоконтролю та самостійної роботи студентів за змістовним модулем 2.3.
1. Скласти лінійний алгоритм обчислення площі трапеції з основами 15 і 17, та висотою 11 см.
2. Описати алгоритм обчислення функції y = x – 4 (для значень x = 1,2,3,4,5).
Дата добавления: 2014-12-03; просмотров: 443; Мы поможем в написании вашей работы!; Нарушение авторских прав |