
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Обчислення НСД і НСК способом канонічного розкладу на прості множники та за алгоритмом Евкліда.
7. У теорії чисел для знаходження НСК і НСД використовують два способи:
1) спосіб розкладу чисел на прості множники. Для знаходження НСД цим способом, який називають способом канонічного розкладу, потрібно розкласти дані числа в добуток простих множників і для знаходження НСД потрібно записати добуток спільних множників у найменшому степені. Для знаходження НСК даних чисел потрібно розкласти ці числа на прості множники, а потім записати добуток всіх простих множників у найбільшому степені.
2) спосіб знаходження НСД, який називають алгоритмом Евкліда. Він ґрунтується на такій теоремі.
Теорема: якщо натуральне число а можна представити у вигляді a=b·q+r, де a,b,q,rєN, то множина спільних дільників чисел a і b співпадає з множиною спільних дільників чисел b і r.
Доведення: нехай a=b·q+r. Позначимо через М множину таких натуральних чисел d, які є дільниками чисел а і b, тобто М={dÎN/a 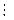 dÙb
dÙb 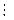 d}. Через К позначимо множину таких натуральних чисел k, які є дільниками чисел b і r, тобто K={kÎN/b
d}. Через К позначимо множину таких натуральних чисел k, які є дільниками чисел b і r, тобто K={kÎN/b 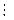 kÙr
kÙr 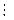 k}. Для доведення теореми нам потрібно показати, що кожен елемент множини M є елементом множини K і навпаки. Отже, доведення складається із двох частин.
k}. Для доведення теореми нам потрібно показати, що кожен елемент множини M є елементом множини K і навпаки. Отже, доведення складається із двох частин.
У першій частині доведемо, що кожен елемент множини M є елементом множини K. Нехай xÎM. Оскільки (a 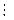 x)Ù(b
x)Ù(b 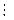 x), то за теоремою про подільність різниці та добутку (a-bq)
x), то за теоремою про подільність різниці та добутку (a-bq) 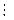 x. Зважаючи на те, що a-bq=r, маємо r
x. Зважаючи на те, що a-bq=r, маємо r 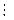 x. Тоді
x. Тоді  . Оскільки елемент х в множині M ми вибирали довільно, то наші міркування можна повторити для кожного елемента множини M, а тому кожен елемент множини M є елементом множини K, тобто MÌK. Перша частина теореми доведена.
. Оскільки елемент х в множині M ми вибирали довільно, то наші міркування можна повторити для кожного елемента множини M, а тому кожен елемент множини M є елементом множини K, тобто MÌK. Перша частина теореми доведена.
У другій частині доведемо, що кожен елемент множини K є елементом множини M. Нехай 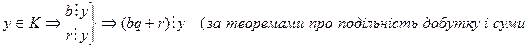 ). Оскільки b·q+r=a, то а
). Оскільки b·q+r=a, то а 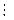 у. Отже,
у. Отже,  . Оскільки елемент y ми вибираємо довільно, то наші міркування можна повторити для кожного елемента множини K. Отже, KÌM. Друга частина теореми доведена.
. Оскільки елемент y ми вибираємо довільно, то наші міркування можна повторити для кожного елемента множини K. Отже, KÌM. Друга частина теореми доведена.
За доведеним у першій частині MÌK, а за доведеним у другій частині KÌM. Відповідно до означення рівності множин випливає, що M=K, тобто множини співпадають. Теорема доведена повністю.
Ця теорема дає можливість звести знаходження НСД для чисел a і b до знаходження НСД чисел b і r, які менші за задані числа. Теоретичною основою цього є наступна теорема.
Теорема: в алгоритмі Евкліда, який застосований до натуральних чисел a і b, остання, відмінна від нуля остача, буде дорівнювати НСД цих чисел.
Доведення: для того, щоб знайти НСД даних чисел за алгоритмом Евкліда треба найбільше число поділити на найменше, потім найменше число на остачу, потім першу остачу на другу і т.д., аж доки не отримаємо в остачі 0. Тоді остання відмінна від 0 остача і буде НСД. Якщо a 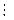 b, то НСД(а,b)=b. Якщо ж а не ділиться націло на b, то відповідно до теореми про ділення з остачею маємо: a=bq+r, де a,b,q,rÎN, a>b>r>r1>r2>…>rk і b=rq1+r1, r=r1q2+r2 тощо. Оскільки ми маємо a>b>r>r1>r2>…>rk, то за принципом найменшого числа ми прийдемо до випадку, коли якесь rk=0, а тому ділення буде виконуватися націло. Тоді НСД(rk-1,0)=rk-1. Теорема доведена.
b, то НСД(а,b)=b. Якщо ж а не ділиться націло на b, то відповідно до теореми про ділення з остачею маємо: a=bq+r, де a,b,q,rÎN, a>b>r>r1>r2>…>rk і b=rq1+r1, r=r1q2+r2 тощо. Оскільки ми маємо a>b>r>r1>r2>…>rk, то за принципом найменшого числа ми прийдемо до випадку, коли якесь rk=0, а тому ділення буде виконуватися націло. Тоді НСД(rk-1,0)=rk-1. Теорема доведена.
Проілюструємо обидва способи знаходження НСД і НСК на таких прикладах.
Вправа 1: знайти НСД(248, 1024) за допомогою канонічного розкладу.
Розв’язання:
Розкладаємо числа 248 і 1024 на прості множники (див. таблицю № 4.9.).
Щоб знайти НСД(248,1024) потрібно записати добуток спільних множників у найменшому степені. Оскільки спільним множником є тільки число 2 у третьому степені, то НСД(248,1024)=23=8.
Вправа 2: знайти НСК(512,90) способом розкладу на прості множники.
Розв’язання:
Розкладаємо числа 512 і 90 на прості множники (див. таблицю № 4.10.).
Щоб знайти НСК(512,90) потрібно записати добуток всіх множників у найбільшому степені. Отже, маємо: НСК(512,90)=29· 32·5=23040.
| 248=23·31 | |||
| 1024=210 |
Таблиця № 4.9.
| 90=2·32·5. | |||
| 512 = 29. |
Таблиця № 4.10.
Вправа 3: знайти НСД(2002,12506) за допомогою алгоритму Евкліда.
Розв’язання:
Використовуючи алгоритм Евкліда для знаходження НСД слід більше число ділити на менше, потім менше число ділимо на першу остачу, потім першу остачу на другу остачу тощо. Цей процес продовжуватиметься доти, доки не отримаємо в остачі 0. При використанні алгоритму Евкліда для знаходження НСД запис потрібно починати з правого боку сторінки. Покажемо це на конкретному прикладі (див. таблицю № 4.11.):
| _12506 12012 | ||
| _ 2002 1976 | ||
| _494 26 | ||
| _234 234 | ||
| Оскільки остання, відмінна від нуля, остача дорівнює 26, то НСД(12506,2002)=26. |
Таблиця № 4.11.
Якщо відомий НСД чисел та самі числа, то для знаходження НСК чисел потрібно використати таку властивість: 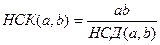 . Отже, НСК(12506,2002)=(12506●2002):26=25037012:26=962962.
. Отже, НСК(12506,2002)=(12506●2002):26=25037012:26=962962.
Дата добавления: 2014-12-03; просмотров: 1135; Мы поможем в написании вашей работы!; Нарушение авторских прав |