
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Необхідність розширення множини цілих чисел.
1. Подальший розвиток людського суспільства довів необхідність розширення множини цілих чисел, бо їх не вистачало як для потреб практики, так і для математики. На практиці зустрічалися випадки, коли неможливо було визначити результат вимірювання чи виконати операцію ділення у випадках виду 20:3. З точки зору математики це означало, що, по-перше, існують несумірні відрізки, по-друге, рівняння виду 7х=48 не має цілих коренів. Все це призвело до виникнення поняття дробу, які виникли із необхідності вимірювання величин та розв’язування рівнянь виду ах=b. Спочатку виникли конкретні дроби, кожен з яких мав свою назву та позначення. Пізніше з’являються основні одиничні дроби виду  (Єгипет). У стародавній Греції з’являються і звичайні дроби.
(Єгипет). У стародавній Греції з’являються і звичайні дроби.
Історія розвитку людства та математики свідчать, що дроби позначали по-різному, але вже у І ст. до н. е. Герон і Діофант застосовували риску дробу, але знаменник писали над рискою дробу, а чисельник – під нею. В У столітті до н.е. греки вміли виконувати всі дії над звичайними дробами. Першим вченим Європи, який застосував риску дробу та сучасний запис дробів, був італійський математики Леонардо Пізанський (або Леонардо Фібоначчи – син Боначчи).
Дроби у стародавній Русі називали долями або ламаними числами, а деякі з них позначали і називали так:  - половина, полтина;
- половина, полтина;  - четь;
- четь;  - полчеть;
- полчеть; 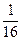 – полполчеть;
– полполчеть;  – полполполчеть (мала четь);
– полполполчеть (мала четь);  - седьмина;
- седьмина;  - треть;
- треть;  – полтреть;
– полтреть;  – полполтреть;
– полполтреть;  – полполполтреть (мала треть);
– полполполтреть (мала треть);  – п’ятина;
– п’ятина;  – десятина тощо. Такий запис та назви існували до ХУІ століття та були витіснені за Петра І.
– десятина тощо. Такий запис та назви існували до ХУІ століття та були витіснені за Петра І.
Десяткові дроби незалежно були винайдені із потреб практики в різні часи в Азії та Європі. Досить повне й систематичне трактування одержують десяткові дроби у працях середньоазіатського вченого аль-Коші в 20-х роках ХУ ст. Незалежно від нього в 80-х роках ХУІ ст. десяткові дроби були «відкриті» заново в Європі нідерландським математиком С.Стевіном. Кома, як знак, що відділяє цілу частину від дробової, вперше була застосована італійським астрономом Дж.Маджині (1555-1617 рр.). Окрім того, німецький математик Хр.Клавіус у 1593 році застосовував для цієї мети крапку.
Розглядаючи цілі числа, ми ввели поняття від’ємних чисел, але поява від’ємних чисел і дробових чисел в практиці повсякденної діяльності та в математиці не співпадають. Історія людства свідчить, що раніше виникли дробові числа, які більше застосовувалися у практичній діяльності людини, ніж від’ємні. Так, від’ємні числа почали застосовуватися лише у І ст. до н. е. у Китаї у зв’язку з розв’язуванням рівнянь. На письмі їх писали чорнилами різних кольорів: додатні числа писали червоним кольором (китайською «чен»), а від’ємні – чорним кольором (китайською «фу»). Індійські математики Брахмагупта (УІІ ст.) та Бхаскара (ХІІ ст.) дали правила дій над від’ємними числами. У Європі від’ємні числа вперше почав використовувати Л.Фібоначчи (ХІІ-ХІІІ ст.). Німецький математик М.Штіфель (ХУІ ст.) називав їх числами меншими, ніж ніщо. Протягом всього цього періоду від’ємні числа називали абсурдними, недійсними тощо. Тільки після того, як у ХУІІ ст. видатний французький вчений Р.Декарт зобразив на числовій прямій додатні числа праворуч, а від’ємні – ліворуч від початку відліку, їх почали визнавати. Отже, розвиток практики та потреби математики з необхідністю вимагають розширення множини цілих чисел.
Таким чином, розширювати множину цілих чисел будемо так, щоб виконувалися наступні вимоги: 1) до нової множини приєднаємо числа нової природи - дробові числа; 2) визначимо арифметичні операції додавання, віднімання, множення і ділення над дробовими числами так, щоб вони не суперечили правилам виконання дій над цілими числами; 3) поширимо основні закони (властивості) дій над цілими числами на числа нової природи; 4) поставимо завдання про необхідність виконання дії ділення (крім ділення на нуль!) для будь-яких чисел нової природи, тобто буде можливість розв’язати рівняння виду ах=b для будь-яких чисел нової множини.
Дата добавления: 2014-12-03; просмотров: 296; Мы поможем в написании вашей работы!; Нарушение авторских прав |