Доведення. Розглянемо дріб і довільне mÎN

Розглянемо дріб 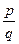і довільне mÎN. Помножимо чисельник і знаменник на m. Одержимо 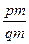. Як показати, що ? – згідно означення про рівні дроби, а це дійсно так, бо p(qm)=q(pm), бо p, q і m ÎN, для яких p(qm)=q(pm), адже справедливі переставний і сполучний закони множення. Аналогічно можна довести і другу частину теореми.

Виявляється, що основна властивість дробів знайшла широке застосування при виконанні таких операцій над дробами як скорочення дробів і зведення дробів до спільного знаменника.

Означення: скороченням дробу називається операція ділення чисельника і знаменника дробу на їхні спільні дільники, в результаті якої дріб замінюється рівносильним йому дробом з меншими числами.

Означення: зведенням дробів до спільного знаменника називається операція множення чисельника і знаменника на одне і те ж саме, відмінне від нуля число, в результаті якої даний дріб замінюється рівносильним йому, але з вказаним знаменником.

Означення: якщо чисельник дробу менший за знаменник, то дріб називають правильним. Якщо чисельник дробу більший за знаменник або дорівнює йому, то дріб називають неправильним.

Означення: дріб називають нескоротним, якщо найбільший спільний дільник чисельника і знаменника дорівнює 1.

Прикладом правильних дробів серед наступних є перший, другий і четвертий, а неправильним є третій. Прикладом нескоротних дробів є наступні