КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сферичний конденсатор
Сферичний конденсатор складається з двох сферичних поверхонь, розділених шаром діелектричної речовини з діелектричною проникністю e (рис.8.5).
Рис.8.5
Напруженість електричного поля на відстані r можна розрахувати, як для точкового заряду
. (8.2.13)
Знайдемо ємність сферичного конденсатора за аналогією з розрахунками ємності плоского і циліндричного конденсаторів.
,
, 
або
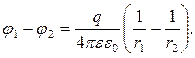(8.2.14)
Вираз (8.2.14) підставимо у (8.2.4), одержимо ємність сферичного конденсатора
. (8.2.15)
Конденсатори різних типів мають досить широке практичне використання.
З’єднання конденсаторів
У випадку, коли до батареї конденсаторів прикладена стала різниця потенціалів ( Dj = const), будемо мати:
а). паралельне з’єднання конденсаторів
. (8.2.16)
б). послідовне з’єднання конденсаторів
,
звідки
. (8.2.17)
8.3. Енергія взаємодії електричних зарядів. Енергія окремого провідника і конденсатора
Енергія системи нерухомих точкових електричних зарядів
Розглянемо систему двох електричних зарядів q1 і q2, які перебувають на відстані r один від одного, кожний з яких в полі другого заряду має потенціальну енергію
;
,
де φ1,2 – потенціал першого заряду в полі другого заряду; φ2,1 – потенціал другого заряду в полі першого заряду.
Оскільки енергії 
і 
- однакові, то енергія системи нерухомих електричних зарядів q1 і q2 буде дорівнювати
. (8.3.1)
Якщо взаємодіють n електричних зарядів, то за аналогією з (8.3.1) будемо мати
. (8.3.2)
де 
- потенціал в точці розміщення і-го заряду, створюваний всіма n зарядами цієї системи.
Вираз (8.3.2) дає можливість розрахувати енергію взаємодії будь-якої системи статичних зарядів.
Енергія зарядженого окремого провідника
Розглянемо окремий провідник, заряд, ємність і потенціал якого відповідно дорівнюють q, C, j. Для зміни потенціалу провідника на величину dj слід виконати елементарну роботу по перенесенню заряду dq з безмежності в дану точку провідника
.
Щоб зарядити провідник від нульового потенціалу до величини j, необхідно виконати роботу
. (8.3.3)
Тому енергія окремого зарядженого провідника визначається формулою
,
а з врахуванням співвідношення 
, будемо мати
. (8.3.4)
Енергія зарядженого конденсатора
Для знаходження енергії зарядженого конденсатора слід розрахувати роботу переміщення заряду q з однієї пластини на іншу пластину.
Елементарна робота зовнішніх сил перенесення малого заряду dq з обкладки 2 конденсатора на обкладку 1 буде дорівнювати
.
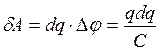Робота переміщення заряду q визначається інтегралом
.
З використанням співвідношення 
, енергія зарядженого конденсатора буде дорівнювати
. (8.3.5)
Оскільки різницю потенціалів двох точок поля 
можна виразити однією буквою U, то формули (8.3.5) матимуть вигляд:
. (8.3.6)
8.4. Енергія електростатичного поля. Густина енергії електро-статичного поля
У загальному випадку електричну енергію системи заряджених нерухомих тіл, провідників і непровідників, можна знайти за формулою:
(8.4.1)
де s і r - відповідно поверхнева і об’ємна густини вільних електричних зарядів; j - потенціал результуючого поля всіх вільних і зв’язаних електричних зарядів, заряджених поверхонь і об’ємів.
Інтегрування виразу (8.4.1) слід здійснювати по всім зарядженим поверхням S і по всьому об’єму V заряджених тіл системи.
Для прикладу знайдемо енергію поля плоского конденсатора. Скористаємось формулою (8.3.6), а саме
.
Для плоского конденсатора
, U=Ed,
де Е – напруженість поля між пластинами конденсатора; d – відстань між пластинами.
В цьму випадку енергія поля зарядженого конденсатора буде дорівнювати:
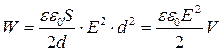, (8.4.2)
де V = Sd – об’єм діелектрика; Е – напруженість електричного поля в діелектрику.
Густину енергії електричного поля в діелектрику можна знайти, поділивши вираз (8.4.2) на об’єм V, тобто
. (8.4.3)
За допомогою формули (8.4.3) знаходять густину енергії електричного поля в об’ємі діелектрика. Її інколи називають об’ємною густиною енергії поля конденсатора.
Вираз (8.4.3) показує, що вся енергія зарядженого конденсатора локалізована в електростатичному полі діелектрика. Цією формулою можна скористатись і для неоднорідних полів.
ЛЕКЦІЯ 9
ЕЛЕКТРИЧНЕ ПОЛЕ В ДІЕЛЕКТРИКУ
9.1. Зв’язані і вільні електричні заряди. Поляризованність діелектрика . Діелектрична сприйнятливість.
9.2. Вектор електричного зміщення. Теорема Гаусса для поля в діелектрику. Діелектрична проникність.
9.3. Поле в діелектрику. Умови на межі двох діелектриків.
9.4. Сегнетоелектрики (самостійно).
9.1. Зв’язані й вільні електричні заряди. Поляризованість
діелектрика. Діелектрична сприйнятливість
Діелектриками (або ізоляторами) називають речовини, які практично не проводять електричний струм. В таких речовинах відсутні вільні електричні заряди.
Однак, це зовсім не означає, що зовнішнє електричне поле не діє на діелектрики. За результатами дії електричного поля на діелектрики останні можна поділити на три групи:
а) полярні діелектрики H2O, NH3, BaTiO3, …
б) неполярні діелектрики H2, N2, CO2, CH4,…
в) іонні кристали NaCl, KCl,…
Зупинимося на більш детальній характеристиці кожної групи діеле-ктриків та дії на них зовнішнього електричного поля.
Полярні діелектрики
Існує ряд діелектриків, в молекулах яких уже від природи зміщені центри позитивних і негативних зарядів у відношенні один до одного. Такі молекули за своєю природою ще називаються диполями. Прикладом дипольної будови може бути молекула води. Атоми водню у такій молекулі створюють ковалентні зв’язки з атомом кисню. Молекула має несиметричний характер (рис. 9.1).
Рис.9.1.
Електричний дипольний момент такої молекули дорівнює добутку величини зміщеного електричного заряду q на відстань між центрами зміщених зарядів.
. (9.1.1.)
Напрям вектора дипольного моменту направлений по лінії від позитивного заряду в сторону негативного заряду, як це показано на рис. 9.1.
У формулі (9.1.1.) величина електричного заряду
.
При внесенні полярного діелектрика у зовнішнє електричне поле він буде поляризуватись. Суть поляризації діелектрика зводиться до орієнтації полярних молекул у напрямку силових ліній електричного поля. Схематично цей процес можна подати за допомогою рис. 9.2.
Е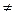 
0
а) б)
Рис.9.2.
На окрему дипольну молекулу зі сторони зовнішнього електричного поля буде діяти пара сил 
, моменти яких направлені від нас за площину рис. 9.3.
Рис.9.3.
Під дією цих моментів молекула повертається і займає положення, при якому її дипольний момент направляється по лінії напруженості (рис.9.4).
Рис.9.4.
Покажемо це за допомогою розрахунків. На електричний диполь буде діяти пара сил 
, момент яких направлений за площину рисунка.
.
Враховуючи, що F = qE, одержимо
,
або
. (9.1.2)
При дії цього моменту сил відбувається повертання дипольної молекули до тих пір, доки 
і 
не будуть орієнтовані вздовж однієї лінії (рис. 9.4).
Реальна картина поляризації полярних діелектриків ускладнюється за рахунок взаємодії між окремими дипольними моментами. В цьому випадку розрахований момент сил в певній мірі зменшується.
Неполярні діелектрики
В неполярних молекулах при відсутності зовнішнього електричного поля центри позитивних і негативних зарядів у межах молекули збігаються.
При внесенні таких молекул у зовнішнє електричне поле вони стають полярними. Це означає, що під дією зовнішнього електричного поля деформуються електронні оболонки молекул (рис. 9.5).
Рис.9.5
Процес поляризації неполярних молекул має пружні властивості, подібно до пружної механічної деформації, яка пояснюється законом Гука.
Дослідним способом установлено, що величина дипольного моменту всіх молекул у зразку діелектрика пропорційна напруженості зовнішнього електричного поля Е, тобто
, (9.1.3)
де e0 – діелектрична стала; c - діелектрична сприйнятливість ( різна для різних діелектриків, безрозмірна величина).
Для діелектриків завжди c>0. Діелектрична сприйнятливість c не залежить від величини напруженості електричного поля Е.
Іонні діелектрики
При внесенні в зовнішнє електричне поле іонних діелектриків (кристали кухонної солі NaCl та інші) кристалічні гратки останніх деформуються. Вузли гратки, які заряджені позитивно, орієнтуються по полю, негативно заряджені вузли орієнтуються проти силових ліній електричного поля.
Таким чином, і в іонних кристалах здійснюється поляризація.
Мірою поляризації діелектрика є відмінний від нуля в об’ємі V дипольний момент діелектрика .
, (9.1.4)
де рі –дипольний момент однієї молекули.
Кількісною мірою поляризації діелектрика є вектор поляризації. Вектором поляризації діелектрика називають електричний момент одиниці об’єму діелектрика.
, (9.1.5)
де V – об’єм діелектрика; 
- векторна сума всіх дипольних моментів окремих молекул в цьому об’ємі.
Помножимо і поділимо (9.1.5) на число окремих диполів у об’ємі V.
, (9.1.6)
де n – концентрація диполів, 
- середнє значення дипольного моменту однієї молекули.
Знайдемо зв’язок між вектором поляризації 
і величиною зв’язаного заряду s¢. Розглянемо діелектричну призму перерізом S і довжиною L, розміщену в зовнішнє електричне поле з напруженістю (рис. 9.6).
Рис. 9.6
Під дією зовнішнього електричного поля у діелектрику відбудеться зміщення електричних зарядів з утворенням поля Е¢. На торцях циліндра появляються заряди +s¢S і -s¢S. Відстань між цими зарядами дорівнює L. Тому електричний момент циліндра буде дорівнювати s¢SL.
Але з другого боку електричний момент всього циліндра чисельно дорівнює значенню суми векторів моментів всіх молекул циліндра, тому
=s¢SL . (9.1.7)
Числове значення вектора поляризації діелектрика можна одержати, якщо поділити (9.1.6) на об’єм циліндра
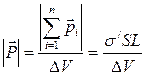. (9.1.8)
Але об’єм циліндра дорівнює
DV = SLcos a , (9.1.9)
де a - кут між напрямком нормалі до циліндра і вектором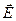 
. Підставимо (9.1.9) у (9.1.8), знайдемо вираз для вектора поляризації 
.
,
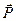звідки
s¢ = Р cos a = Рn,
де Рn – проекція вектора поляризації на нормаль до поверхні циліндра.
Тому
s¢=Рn, (9.1.10)
Густина поверхневих зв’язаних зарядів s¢ чисельно дорівнює перпендикулярній складовій вектора поляризації. З урахуванням співвідношення (9.1.3) одержимо, що
s¢ = ce0Еn¢. (9.1.11)
9.2. Вектор електричного зміщення. Теорема Гаусса для поля в
діелектрику. Діелектрична проникність
Розглянемо діелектрик, який розміщено між пластинами конденсатора, площа яких досить велика порівняно з відстанню між пластинами. Лише при цій умові електричне поле в центральній частині конденсатора можна вважати однорідним (рис. 9.7).
З рисунка видно, що електричне поле 
, створюється вільними зарядами, розміщеними на пластинах конденсатора. Електричне поле 
створено зв’язаними електричними зарядами. Вектор поляризації 
безпосередньо відноситься до вільних зарядів на пластинах конденсатора.
Рис.9.7
В діелектрику поля 
і 
паралельні, тому результуюче поле визначається за допомогою принципу суперпозиції
+ .
В скалярній формі
| 
|=Е0-Е¢,
де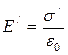 
.
Скористаємося теоремою Гаусса до замкнутої поверхні у вигляді циліндра з стороною h паралельною до вектора 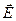. Нехай висота циліндра h»0, тоді
,
де Е = Е0 - 
.
З урахуванням того, що Е¢ і Рn мають протилежні знаки, одержимо (рис. 9.7)
(9.2.1)
Помножимо рівняння (9.2.1) на e0, одержимо:
. (9.2.2)
Величину в дужках в лівій частині рівняння називають вектором електричного зміщення і позначають буквою 
.
. (9.2.3)
Вектор електричного зміщення визначається лише вільними зарядами і не залежить від властивостей діелектрика.
Теорема Гаусса для поля в діелектрику буде мати вигляд
. (9.2.4)
Із викладеного вище відомо, що
=ceо 
о.
Підставимо величину вектора поляризації 
у співвідношення (9.2.3), одержимо
. (9.2.5)
Величину 1+c у співвідношенні (9.2.5) називають відносною діелектричною проникністю середовища і позначають буквою e, тобто
e= 1+c . (9.2.6)
З урахуванням (9.2.6) вектор електричного зміщення буде мати вигляд
(9.2.7)
Для вакууму e =1; в діелектричному середовищі e >1.
Фізично відносна діелектрична проникність середовища показує у скільки разів напруженість електричного поля у вакуумі більша за напруженість цього ж поля у деякому діелектричному середовищі.
9.3. Поле в діелектрику. Умови на межі двох діелектриків
Розглянемо плоский конденсатор, заповнений діелектриком (рис.9.8).
Рис.9.8
На рисунку s - поверхнева густина вільних електричних зарядів на обкладках конденсатора; s¢ - поверхнева густина зв’язаних зарядів діелектрика.
В цьому випадку
,
в той же час
.
Для поля в діелектрику одержимо співвідношення
. (9.3.1)
Напруженість поля у діелектрику збігається з напруженістю поля у вакуумі у випадку рівності s = s¢.
Для вимірювання поля у діелектрику достатньо виміряти різницю потенціалів на обкладках конденсатора і відстань між пластинами конденсатора.
У цьому випадку
. (9.3.2)
Розглянемо умови на межі двох діелектриків. На межі поділу двох діелектриків з різними діелектричними проникностями вектори 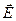і можуть стрибкоподібно змінювати свою величину. Розглянемо цей процес дещо детальніше.
Рис.9.10
Поблизу межі поділу в кожному із діелектриків електричні поля створені лише зв’язаними зарядами. Ці поля орієнтовані в різних напрямках.
Результуюче поле 
в цьому випадку буде дорівнювати
= 
. (9.3.3)
Скористаємось теоремою Гаусса для розрахунку потоку напруженості електричного поля крізь замкнуту поверхню циліндра з торцями S і висотою h (всі розміри досить малі)
.
Тут вільні електричні заряди відсутні, а тому й права сторона співвідношення дорівнює нулю.
Після інтегрування одержимо
Dn,2S = Dn,1S ,
або
Dn,2 = Dn,1 (9.3.4)
Нормальні складові електричного зміщення на межі поділу двох
діелектриків не розриваються.
З урахуванням того, що Dn,2 = e2e0En,2, а Dn,1 = e1e0En,1, одержуємо:
e2e0En,2 = e1e0En,1,
звідки
,
тому
Еn,1 ¹ En,2 . (9.3.5)
Нормальні складові напруженостей електричного поля на межі поділу двох діелектриків розриваються.
Для дослідження дотичних складових векторів 
і 
на межі поділу двох діелектриків можна скористатися теоремою про циркуляцію вектора .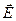
Рис. 9.11
У вибраному прямокутнику довжина сторони h наближено дорівнює нулю, тому
.
Після інтегрування одержимо
.
Дотичні складові вектора напруженості на межі поділу двох діелектриків не розриваються.
Для дотичних складових вектора електричного зміщення будемо мати
.
Так як e1¹e2, то
.
Дотичні складові електричних зміщень розриваються на межі поділу двох діелектриків.
ЛЕКЦІЯ 10
ПОСТІЙНИЙ ЕЛЕКТРИЧНИЙ СТРУМ
10.1. Провідники й ізолятори. Електричний струм. Умови існування струму. Сторонні сили.
10.2. Закон Джоуля-Ленца в інтегральній формі. Опір провідників. Потужність струму.
10.3. Закони Ома для ділянки кола, неоднорідної ділянки кола і замкнутого кола. Правила Кірхгофа.
10.4. Закони Ома й Джоуля-Ленца в диференціальній формі. Густина електричного струму в провідниках.
10.1. Провідники і ізолятори. Електричний струм. Умови існування струму. Сторонні сили
До провідників відносять будь-які речовини, які мають вільні електричні заряди незалежно від агрегатного стану і від умов оточуючого середовища. Деякі речовини стають провідниками лише при підвищенні температури, а при досить високих температурах практично всі речовини є провідниками.
Ізолятори – це речовини, які при звичайних умовах не мають вільних зарядів, або їх число можна вважати безмежно малим.
Електричний струм – це направлений рух електричних зарядів, які приводяться в рух електричним полем або рухаються на протидію електричному полю. Чисельно електричний струм характеризують швидкістю переміщення електричних зарядів, тобто
I = 
.
Електричний струм вимірюється в амперах (А). Струм в 1А відповідає заряду в 1Кл, який переноситься через поперечний переріз провідника за час в 1с.
Одиниця електричного струму в 1А є основною одиницею системи СІ, а тому має більш загальне визначення, яке буде розглянуте пізніше.
Для існування електричного струму необхідне виконання певних умов, серед яких:
а) наявність провідника;
б) наявність джерела електрорушійної сили;
в) наявність замкнутого кола.
Невиконання цих умов, або будь-якої із них, робить неможливим виникнення електричного струму в провіднику.
У джерелі струму перерозподіл зарядів на його клемах здійснюється за допомогою сторонніх сил, тобто сил неелектричного походження.
У випадку замкнутого провідника сили електричного походження роботи не виконують. Робота таких сил дорівнює нулю. Перерозподіл зарядів у джерелі здійснюється переважно силами хімічного, магнітного, механічного, й іншого походження. У цьому випадку в джерелі одночасно існують два електричні поля:
- зовнішнє поле 
, утворене різницею потенціалів між клемами джерела;
- внутрішнє, або поле сторонніх сил * 
, яке діє лише у джерелі (рис.10.1).
Рис.10.1
Струм І існує у зовнішній ділянці кола і створюється полем 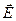. Струм 
існує у джерелі і створюється полем сторонніх сил 
.
На будь-який заряд у цьому випадку діятиме сила, величина якої дорівнює
= 
. (10.1.1)
Під дією цієї сили виконується елементарна робота
= 
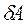. (10.1.2)
З урахуванням (10.1.1) елементарна робота 
буде дорівнювати:
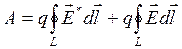, (10.1.3)
де 
- теорема про циркуляцію вектора .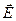
Тому величину 
- називають електрорушійною силою джерела струму, тобто
. (10.1.4)
Електрорушійна сила джерела струму чисельно дорівнює роботі переміщення точкового електричного заряду сторонніми силами в замкнутому колі, включаючи і саме джерело, до величини цього заряду, тобто
(10.1.5)
Причиною виникнення е. р. с. джерела струму може бути також змінне в часі магнітне поле, що видно із одного із рівнянь Максвелла
, (10.1.6)
де 
- змінне в часі магнітне поле; 
- потік змінного в часі магнітного поля крізь довільну замкнуту поверхню в перпендикулярному напрямку до цієї поверхні. Це та інші рівняння Максвелла будуть розглянуті в наступній лекції.
10.2. Закон Джоуля-Ленца в інтегральній формі. Опір провідників. Потужність струму
Найпростішою формою дії струму в провіднику є його теплова дія. Дослідним шляхом установлено, що:
а) кількість теплової енергії, яка виділяється у провіднику, прямо пропорційна часу дії струму, тобто dQ ~ dt;
б) величина теплової енергії струму пропорційна квадрату струму в провіднику, тобто dQ ~ І2.
З урахуванням цих двох дослідних фактів можна зробити висновок, що кількість теплової енергії, яка ввиділяється у провіднику завдяки дії електричного струму, пропорційна квадрату струму й часу його протікання, тобто
dQ ~ I2dt . (10.2.1)
Якщо у співвідношення (10.2.1) ввести коефіцієнт пропорційності, то одержимо рівність
dQ = RI2dt. (10.2.2)
Рівність (10.2.2) називають законом Джоуля-Ленца в інтегральній формі. Коефіцієнт пропорційності в цьому законі називають електричним опором провідника.
З рівності (10.2.2) опір провідника буде дорівнювати
, (10.2.3)
де dQ – кількість теплової енергії, яка переноситься електричним струмом; І2 – квадрат величини електричного струму; dt – час проходження струму.
Розмірність електричного опору відповідно до (10.2.3) має значення
.
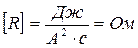Опір провідників вимірюється в омах (Ом).
Встановимо фізичну суть опору провідника, який має вільні електричні заряди, що у випадку відсутності електричного поля рухаються хаотично між вузлами кристалічної гратки з досить великими швидкостями. Середнє значення швидкості хаотичного руху електронів у металевому провіднику приблизно дорівнює 106 м/с.
Температура на швидкість хаотичного руху носіїв струму в провіднику практично не впливає.
Рис.10.2
На рис.10.2 схематично показано ділянку кристалічної структури. Простір між вузлами кристалічної гратки заповнений вільними електронами.
Електричний опір провідника чисельно дорівнює роботі, яка виконується сторонніми силами джерела струму для подолання хаотичності руху вільних електронів, взаємодії їх один з одним і з вузлами кристалічної гратки.
Слід відмітити, що найбільше енергії джерела струму витрачається на подолання взаємодії носіїв струму з позитивно зарядженими вузлами кристалічної гратки. В меншій мірі енергія джерела витрачається на подолання хаотичності руху й взаємодії носіїв між собою.
У масштабах країни на подолання електричного опору в лініях електропередач витрачається до 25% виробленої електричної енергії.
Опір провідників зростає при їх нагріванні. Пояснити це зростання опору можна збільшенням амплітуди коливань вузлів кристалічної гратки, і як наслідок, зростанням частоти захоплення вузлами кристалічної гратки вільних електричних зарядів. На хаотичність руху носіїв і взаємодію їх один з одним зростання температури практично не впливає (буде пояснено в 3-й частині курсу фізики).
Вираз для потужності електричного струму можна отримати із рівності (10.2.2).
У випадку нерухомого провідника робота струму дорівнює тепловій енергії, тому потужність струму буде дорівнювати
. (10.2.4)
З цієї рівності видно, що величина потужності струму пропорційна квадрату струму, що протікає в колі.
10.3. Закони Ома для ділянки кола, неоднорідної ділянки кола й замкнутого кола. Правила Кірхгофа
Розглянемо неоднорідну ділянку кола, опір якої дорівнює R + r (рис.10.3).
Рис.10.3
На кінцях такої ділянки створена різниця потенціалів j1 - j2. Робота переміщення заряду dq вздовж цієї ділянки дорівнює
, (10.3.1)
де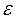 
- електрорушійна сила джерела струму; 
- різниця потенціалів на кінцях провідника.
Якщо ж провідник нерухомий, то цю ж роботу можна виразити із закону Джоуля-Ленца, тобто
, (10.3.2)
де 
- загальний опір ділянки кола й джерела струму; І – величина струму в ділянці кола; dt – час проходження струму.
Прирівняємо праві сторони цих рівностей
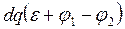
. (10.3.3)
Але заряд dq можна виразити через струм І і час проходження струму dt, тобто
. (10.3.4)
Підставимо вираз (10.3.4) у (10.3.3) і після відповідного скорочення одержимо:
= 
,
звідки
. (10.3.5)
Рівність (10.3.5) називається законом Ома для неоднорідної ділянки кола, тобто ділянки кола , яка містить електрорушійну силу джерела e.
У випадку відсутності електрорушійної сили e у колі одержимо закон Ома для ділянки кола
. (10.3.6)
Якщо коло замкнуте, то j1- j2 = 0, тому що початкова й кінцева точки збігаються. У такому випадку одержимо закон Ома для замкнутого кола, тобто
. (10.3.7)
Закономірності (10.3.5), (10.3.6) і (10.3.7) називаються законами Ома в інтегральній формі. Ці закони мають широке практичне використання для розрахунку електричних кіл в електротехніці.
Розглянемо ділянку розгалуженого кола, яке складається з трьох неоднорідних ділянок АВ, ВС і СА (рис.10.4)
На цьому рисунку точки А,В,С називаються вузловими точками. В ці точки входять і виходять не менше трьох струмів. Для вузлових точок у відповідності із законом збереження електричних зарядів, має виконуватись умова, згідно з якою
. (10.3.8)
Рівність (10.3.8) називають першим правилом Кірхгофа. Суть цього правила така:
Алгебраїчна сума всіх струмів будь-якої вузлової точки розгалуження дорівнює нулю.
Рис.10.4
Запишемо закон Ома для кожної окремої неоднорідної ділянки кола (рис. 10.4):
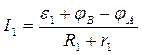, (10.3.9)
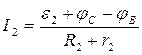, (10.3.10)
. (10.3.11)
Зведемо рівності (10.3.9) – (10.3.11) до спільного знаменника й додамо їх
І1(R1+r1) + I2(R2+r2) + I3(R3+r3) = e1+ e2+ e3,
або
, (10.3.12)
де 
- алгебраїчна сума всіх спадів напруг в замкнутому колі; 
- алгебраїчна сума електрорушійних сил в цьому колі.
Рівність (10.3.12) називається другим правилом Кірхгофа. Правила Кірхгофа значно полегшують розрахунки розгалужених кіл і широко використовуються в електротехнічних дисциплінах.
10.4. Закони Ома й Джоуля-Ленца в диференціальній формі. Густина електричного струму в провіднику
Розглянемо елемент провідника перерізом S і довжиною 
. Концентрація вільних електронів у такому провіднику дорівнює n (рис.10.5)
Рис.10.5
Нехай в такому елементі за допомогою сторонньої сили джерела e створений струм І. Величина струму в провіднику буде дорівнювати:
, (10.4.1)
де 
- число зарядів у елементі провідника з об’ємом 
; n – концентрація вільних електронів; qo – елементарний електричний заряд; 
- середня швидкість направленого руху носіїв струму.
Розрахунки показують, що 
наближено кілька міліметрів за секунду. Це дуже мала швидкість. Швидкість хаотичного руху електронів у металевому провіднику при звичайних умовах має порядок 106 м/с.
Густину струму провідності в провіднику легко знайти, поділивши (10.4.1) на переріз провідника S
. (10.4.2)
Розрахунки показують, що у кабелі з двох жил перерізом 1 мм2 безпечним є струм, який не перевищує величини (12,5 ¸ 15)А. Якщо цей струм, а також концентрацію вільних носіїв струму, яка для більшості провідників не перевищує 1029 м-3 , підставити у формулу (10.4.2), то одержимо значення швидкості направленого руху електронів. Ця швидкість буде дорівнювати лише кілька міліметрів за секунду. В процесі направленого руху носії струму більшість часу перебувають у вузлах кристалічної решітки.
Знайдемо середню швидкість направленого руху носіїв струму у провіднику, які рухаються під дією сторонніх сил джерела струму.
Будемо вважати, що між двома сусідніми взаємодіями з вузлами кристалічної решітки носії струму рухаються з прискоренням a. Нехай між двома сусідніми взаємодіями кожен з електронів вільно рухається протягом часу t. Перед взаємодією швидкість електрона досягає максимального значення umax Вириваючись із вузла решітки швидкість електрона дорівнює нулю.
Тому середня швидкість направленого руху електрона між двома сусідніми взаємодіями буде дорівнювати
. (10.4.3)
Оскільки рух рівноприскорений, то
umax = at.
Прискорення руху носіїв струму простіше знаходити із 2-го закону Ньютона, тобто
qоE = ma,
звідки
а = 
.
Тому
umax = 
, (10.4.4)
де qo – елементарний заряд; Е – напруженість електричного поля у провіднику; t - час вільного руху між двома взаємодіями; m – маса електрона.
Підставимо (10.4.4) у (10.4.3), одержимо
. (10.4.5)
Значення середньої швидкості підставимо у формулу (10.4.2), одержимо закон Ома у диференціальній формі
, (10.4.6)
де n – концентрація вільних носіїв струму у провіднику; q0 – величина елементарного заряду; τ – час вільного руху носіїв струму між двома сусідніми взаємодіями; m- маса носія струму у провіднику (у більшості випадків це маса електрона).
Величину s = 
називають питомою електропровідністю провідника.
Знайдемо енергію, яка переноситься вільними електричними зарядами у провіднику одиничного об’єму, за одиницю часу, тобто
, (10.4.7)
де w - енергія, яка переноситься електронами одиниці об’єму провідника за одиницю часу.
Оцінити цю енергію можна так. За одиницю часу кожен з електронів захоплюється вузлами кристалічної гратки 
разів, щоразу передаючи гратці кінетичну енергію 
. Оскільки в одиниці об’єму провідника міститься n вільних електронів, то енергія, яка переноситься всіма електронами одиниці об’єму провідника за одиницю часу буде дорівнювати
, (10.4.8)
де n – концентрація вільних електронів у провіднику; 
- число взаємодій кожного із електронів протягом 1с з вузлами кристалічної гратки провідника; 
- кінетична енергія, яка щоразу передається кожним із електронів в процесі взаємодії з вузлами кристалічної гратки.
Підставивши в (10.4.8) значення umax із (10.4.4), одержимо закон Джоуля-Ленца в диференціальній формі
, (10.4.9)
або
w = sЕ2. (10.4.10)
ЛЕКЦІЯ 11
МАГНЕТНЕ ПОЛЕ У ВАКУУМІ
11.1. Магнетне поле. Магнетна індукція. Закон Ампера.
11.2. Закон Біо-Савара-Лапласа та його використання в найпростіших випадках:
а) Магнетне поле прямолінійного провідника із струмом;
б) Магнетне поле кругового провідника із струмом;
в) Магнетне поле соленоїда.
11.3. Магнетний момент контуру із струмом.
11.1. Магнетне поле. Магнетна індукція. Закон Ампера
Дослідним шляхом установлено, що подібно до електричних зарядів, навколо яких виникає електричне поле, в просторі навколо провідників із струмом або постійних магнетів виникає магнетне поле. Магнетне поле – це одна із форм існування матерії, завдяки якій здійснюється взаємодія струмів і постійних магнетів.
Встановлено також, що:
- магнетне поле діє лише на рухомі електричні заряди;
- рухомі електричні заряди створюють у просторі магнетне поле;
- магнетне поле не діє на статичні заряди.
Характер дії магнетного поля на струм залежить:
- від форми провідника, по якому тече струм;
- від розміщення провідника в просторі.
У якості пробного тіла для дослідження магнетного поля використовують замкнутий пробний контур з струмом, лінійні розміри якого досить малі. Магнетне поле такого пробного контуру не повинно створювати зовнішнього магнетного поля. При розміщенні такої рамки у досліджуване зовнішнє магнетне поле, із сторони останнього, на рамку діятиме обертальний момент сил М. Елементарна рамка із струмом займе певний напрям у просторі так, щоб магнетне поле рамки і досліджуваного магнетного поля збігалися (рис 11.1).
Рис11.1
Орієнтація контуру в просторі характеризується напрямком нормалі 
до контуру.
Додатний напрям нормалі визначається правилом правого гвинта. За позитивний напрям нормалі приймається напрям поступального руху правого гвинта, обертання якого збігаються з напрямком струму в пробній рамці.
За напрям магнетного поля у даній точці простору приймається напрям, вздовж якого направляється позитивно орієнтована нормаль до контуру.
Момент сил, який створюється зовнішнім магнетним полем у рамці із струмом, визначається векторним добутком вектора магнетного моменту рамки із струмом і магнетної індукції зовнішнього магнетного поля
, (11.1.1)
де 
- магнетний момент пробної рамки із струмом I і площею S; 
- вектор магнетної індукції – силова характеристика зовнішнього магнетного поля.
Скалярна величина вектора моменту сили 
визначається формулою
. (11.1.2)
Якщо в дану точку зовнішнього магнетного поля розміщувати елементарні рамки із різними магнетними моментами 
, то на них з сторони магнетного поля будуть діяти різні обертальні механічні моменти сил 
. Однак відношення 
для кожного випадку буде сталою величиною, яка є силовою характеристикою цього поля. Позначають цю величину буквою 
і називають індукцією магнетного поля.
. (11.1.3)
Індукція магнетного поля вимірюється у теслах (Тл), розмірність якого визначається з (11.1.3)
.
Подібно до електричного поля магнетне поле зображають з допомогою силових ліній магнетного поля, напрям яких у кожній точці поля збігається із напрямком вектора 
.
Лінії індукції магнетного поля завжди замкнуті й охоплюють провідники із струмом. Замкнутість силових ліній магнетного поля характеризує вихровий характер цього поля.
Природа магнетного поля зводиться або до руху електричних зарядів, або до змінного в часі електричного поля. Про це свідчать рівняння Максвела:
а) 
, (11.1.4)
де 
- циркуляція вектора електростатичного поля вздовж довільного замкнутого контуру; 
- потік змінного в часі вихрового магнетного поля крізь довільну замкнуту поверхню;
б) 
, (11.1.5)
де 
- струм провідності, який створюється в провіднику вільними електричними зарядами;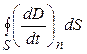 
- потік змінного в часі електричного поля, що інколи називають струмом зміщення. Струм зміщення не пов’язаний з рухом будь-яких електричних зарядів.
Рівняння Максвелла (11.1.4) і (11.1.5) характеризують взаємозв’язок електричних і магнетних явищ. З рівняння (11.1.4) чітко видно, що змінне в часі магнетне поле є причиною виникнення вихрового електричного поля. Останнє, створює електричний струм у замкнутому провіднику.
З рівняння (11.1.5) випливає, що причиною виникнення магнетного поля може бути або струм провідності, або змінне в часі електричне поле, яке не обов’язково призводить до руху зарядів у провіднику.
Оскільки будь-який струм є причиною виникнення магнетного поля, то це пояснює дослідний факт силової дії магнетного поля на провідник із струмом.
Величину цієї сили знайшов Ампер, тому вона називається силою Ампера
, (11.1.6)
де 
- вектор елементу струму, що збігається з напрямком струму у провіднику; 
- індукція зовнішнього магнетного поля.
Рис.11.2
На рис.11.2 струм створюється позитивними зарядами, напрям руху яких збігається з напрямком струму.
Напрям сили Ампера визначається правилом лівої руки. Якщо силові лінії магнетного поля входять в долоню лівої руки, а чотири пальці направлені по напрямку струму у провіднику, то великий палець, відхилений на 900, покаже напрямок сили Ампера.
11.2. Закон Біо-Савара-Лапласа та його використання у найпростіших випадках
Ще на початку 19-го сторіччя французькі фізики Біо і Савар, обробляючи величезний експериментальний матеріал вивчення характеристик магнетного поля провідників зі струмом за участю математика Лапласа, одержали формулу, яка дістала назву у фізиці закону Біо-Савара-Лапласа.
У векторній формі цей закон має вигляд
, (11.2.1)
де m - відносна магнетна проникність середовища, безрозмірна величина; mо – магнетна постійна ( 
); I – струм у провіднику; 
- елемент провідника; 
- відстань від елемента струму до точки, в якій знаходиться індукція магнетного поля 
(рис.11.3).
Рис.11.3
З видно, що вектор індукції магнетного поля 
є дотичною до силової лінії магнетного поля, яка охоплює провідник, і проходить через точку, в якій визначається індукція магнетного поля.
Напрям силової лінії визначається за допомогою правила правого гвинта, як це показано на рисунку.
Поряд із індукцією магнетного поля 
магнетне поле характеризується напруженістю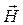 
. Ця величина не залежить від властивостей середовища і дорівнює
. (11.2.2)
Величина напруженості магнетного поля входить в одне із рівнянь Максвелла. Розмірність напруженості 
буде встановлена трохи пізніше.
Закон Біо – Савара - Лапласа для напруженості магнетного поля Н має вигляд
, (11.2.3)
або в скалярній формі
. (11.2.4)
Магнетному полю властивий принцип суперпозиції. Це означає, що поля від кількох джерел магнетного поля накладаються як вектори, тобто
. (11.2.5)
Знайдемо індукцію магнетного поля біля безмежного прямого провідника із струмом (рис.11.4).
Скористаємось законом Біо – Савара - Лапласа в скалярній формі
, (11.2.6)
де кут a - це кут між напрямком елемента провідника із струмом 
і радіусом-вектором 
, як це показано на рис.11.4; 
- дотичний вектор до силової лінії, напрям якого збігаються з напрямком обертання правого гвинта.
Рис.11.4
З рисунка видно, що
dS=dlsina і dS=rda,
звідки
.
Радіус-вектор 
також можна виразити через ro і кут a, тобто
.
З урахуванням цих зауважень закон Біо – Савара - Лапласа набуде вигляду
. (11.2.7)
Інтегруємо вираз (11.2.7) в межах зміни кута a від a1 до a2, в результаті чого одержимо
. (11.2.8)
Якщо у виразі (11.2.8) a1 прямує до 0, а a2 прямує до p, то одержимо безмежний прямий провідник із струмом.
У цьому випадку:
а) індукція магнетного поля буде дорівнювати
. (11.2.9)
б) напруженість магнетного поля буде дорівнювати
. (11.2.10)
З останньої формули легко встановити розмірність напруженості магнетного поля
.
Знайдемо магнетне поле на осі кругового витка із струмом (рис.11.5).
Рис.11.5
Елемент провідника із струмом dl, створює на осі x індукцію магнетного поля dB. Вектор є дотичним до силової лінії, зображеної на рисунку пунктирною лінією. Складова вектора індукції магнетного поля dBy буде скомпенсована аналогічним елементом з протилежної сторони. Результуючу індукцію магнетного поля від кругового витка із струмом слід шукати в напрямку осі x (принцип суперпозиції магнетних полів).
З рисунка видно, що
Дата добавления: 2014-12-03; просмотров: 250; Мы поможем в написании вашей работы!; Нарушение авторских прав