
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
З рисунка видно, що
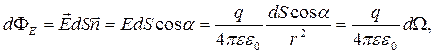
де  - тілесний кут.
- тілесний кут.
Площа поверхні кулі  (тут
(тут  є тілесним кутом).
є тілесним кутом).
Таким чином одержуємо:
 . (6.3.8)
. (6.3.8)
Інтегруємо цей вираз у межах замкнутої поверхні і повного тілесного кута для цієї поверхні, тобто
 .
.
Одержаний вираз носить назву теореми Гаусса
 . (6.3.9)
. (6.3.9)
Якщо замкнута поверхня охоплює систему зарядів, теорема Гаусса набуде вигляду
 . (6.3.10)
. (6.3.10)
Потік вектора напруженості електричного поля крізь довільну замкнуту поверхню дорівнює алгебраїчній сумі всіх зарядів у середині цієї поверхні, поділених на ee0.
Покажемо на прикладах, як використовується теорема Гаусса у найпростіших випадках.
Приклад 1. Електричне поле біля безмежної, рівномірно зарядженої, із поверхневою густиною зарядів σ, площини ( рис. 6.10).

Рис. 6.10
На рисунку заряджена площина спроектована перпендикулярно до площини листка. Замкнена поверхня є циліндром із площею торців S. Потік вектора напруженості в даному випадку слід розрахувати лише крізь торці. Лінії напруженості електричного поля паралельні до бокової поверхні, а тому потоку не створюють, тобто
 . (6.3.11)
. (6.3.11)
За теоремою Гаусса
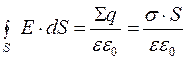 . (6.3.12)
. (6.3.12)
Прирівнявши праві сторони (6.3.11) і (6.3.12) одержимо:
 .
.
Цей висновок збігається з формулою (6.3.3).
Приклад 2. Електричне поле на відстані a від довгої, рівномірно зарядженої з лінійною густиною зарядів τ, нитки (рис. 6.11).

Рис. 6.11
На рисунку замкнуту поверхню вибрано у вигляді циліндра радіусом а і довжиною h. Потік силових ліній слід розглядати лише крізь бокову поверхню, так як торці перпендикулярні до нитки й паралельні до напрямку силових ліній електричного поля. (Потік крізь торці в цьому випадку дорівнює нулю).
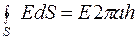 . (6.3.13)
. (6.3.13)
Дата добавления: 2014-12-03; просмотров: 258; Мы поможем в написании вашей работы!; Нарушение авторских прав |