Аксиомы статики.

Все теоремы и уравнения статики выво­дятся из нескольких исходных положений, принимаемых без матема­тических доказательств и называемых аксиомами или принципами статики. Аксиомы статики представляют собою результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой. Часть из этих аксиом является следствиями основных законов механики, с которыми мы познакомимся в динамике.

Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F₁ = F₂) и направлены вдоль одной прямой в противоположные стороны (рис. 2).

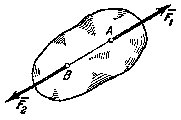Аксиома 1 определяет простейшую уравновешенную систему сил, так как опыт показывает, что свободное тело, на которое действует только одна сила, находиться в равнове­сии не может.

Аксиома 2. Действие данной си­стемы, сил на абсолютно твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему

сил.

Эта аксиома устанавливает, что две системы сил, Рис. 2

отличающиеся на уравнове­шенную систему, эквивалентны друг другу.

Следствие из 1-й и 2-й аксиом. Действие силы на абсо­лютно твердое тело не изменится, если перенести точку при­ложения силы вдоль ее линии действия в любую другую точку тела.

В самом деле, пусть на твердое тело действует приложенная в точке А сила F (рис. 3). Возьмем на линии действия этой силы произвольную точку В и приложим к ней две уравновешенные силы F₁ и F₂, такие, что F₁ = F, F₂ = -F. От этого действие силы F на тело не изменится. Но силы F и F₂ со­гласно аксиоме 1 также образуют уравновешенную систему, которая может быть отброшена. В резуль­тате на тело. Будет действовать

только одна сила F₁, равнаяF, но приложен­ная в точке В. Рис. 3

Таким образом, вектор, изобра­жающий силуF, можно считать приложенным в любой точке на линии действия силы (такой вектор называется скользящим).

Аксиома 3 (аксиома параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующею, приложенную в той же точке и изображаемую диагональю па­раллелограмма, построенного на этих силах, как на сторонах.

Вектор R, равный диагонали параллелограмма, построенного на векторах F₁ и F₂ (рис. 4), называется геометрической суммой векторов F₁ и F₂:

R = F₁ + F₂.

Следовательно, аксиому 3 можно еще формулировать так: две силы, приложенные к телу в одной точке, имеют равнодействую­щую, равную геометрической (векторной) сумме этих сил и прило­женную в той же точке.

Аксиома 4. При всяком действии одного Рис. 4