Тема 5. Численные методы решения обыкновенных дифференциальных уравнений и систем.

1. Решить аналитически задачу Коши:

а) ; б) ;

в) .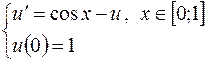

2. Даны два приближенных решения задачи Коши, полученные с помощью схемы Рунге-Кутта 4 порядка точности.

Первое решение:

x= 0.0000000000E+00 u= 1.0000000000E+00

x= 5.0000000000E-01 u= 1.6484375000E+00

x= 1.0000000000E+00 u= 2.7173461914E+00

Второе решение:

x= 0.0000000000E+00 u= 1.0000000000E+00

x= 2.5000000000E-01 u= 1.2840169271E+00

x= 5.0000000000E-01 u= 1.6486994690E+00

x= 7.5000000000E-01 u= 2.1169580259E+00

x= 1.0000000000E+00 u= 2.7182099392E+00

Используя правило Рунге оцените погрешность второго решения в совпадающих узлах сеток.

3. Дана краевая задача:

,

.

Найти аналитически ее решение.

4. Дана краевая задача:

,

.

Опишите, каким образом можно вычислить приближенное решение этой краевой задачи баллистическим методом, имея в своем распоряжении программу, позволяющую получить приближенное решение любой задачи Коши для системы обыкновенных дифференциальных уравнений с любой заданной точностью.

5. Найти аналитически точное решение задачи Коши:

6. Найти точное решение краевой задачи:

а) ; б)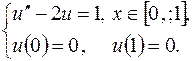

7. Дана краевая задача:

, ,

, .

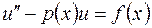Будем считать, что у нас есть программа для вычисления приближенного решения этой краевой задачи разностным методом при заданном значении числа отрезков разбиения N. Опишите, каким образом можно подобрать значение N так, чтобы погрешность приближенного решения этой задачи, полученного с помощью этой программы, не превышала заданного положительного числа ?