Тема 2. Наилучшее среднеквадратическое приближение. Тригонометрическая интерполяция. Наилучшее равномерное приближение.

1. Разложить в тригонометрический ряд Фурье функцию 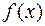. Изобразить график периодическго (с периодом ) продолжения функции . Установить к чему сходится ряд Фурье. Найти наилучшее среднеквадраническое приближение функции на в множестве тригонометрических многочленов 1-ой степени.

а) ; б) ;

в) .

2. Найти наилучшее среднеквадратичное приближение функции , определенной на отрезке 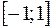, в семействе многочленов вида .

а) ; б) ; в) .

3. Дана таблица значений , некоторой функции . Значения эти имеют значительные погрешности. Методом наименьших квадратов строится наилучшее приближение 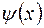в семействе нелинейных функций . Показать как строится это приближение. Определить меру близости между и , в смысле которой это приближение будет наилучшим.

а) ; б) ; в) ;

г) .

4. Построено два приближения , в разных семействах нелинейных или линейных функций методом наименьших квадратов. Как определить какое из них является лучшим?