Тема 3. Численное дифференцирование. Метод Рунге-Ромберга.

1. Как организовать вычисление первой производной с использованием формул численного дифференцирования, имеющих первый порядок точности?

2. Как организовать вычисление первой производной с использованием формул численного дифференцирования, имеющих второй порядок точности?

3. Как организовать вычисление второй производной с использованием формул численного дифференцирования, имеющих второй порядок точности?

4. Найти порядок точности и оценку погрешности формулы 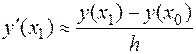при условии, что функция 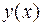имеет ограниченную производную второго порядка на .

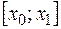5. Найти порядок точности и оценку погрешности формулы 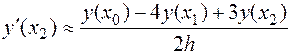при условии, что функция 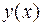имеет ограниченную производную третьего порядка на .

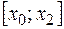6. Найти порядок точности и оценку погрешности формулы 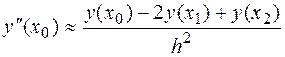при условии, что функция 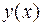имеет ограниченную производную третьего порядка на .

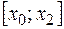7. Найти порядок точности и оценку погрешности формулы 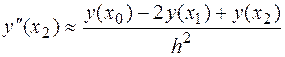при условии, что функция 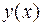имеет ограниченную производную третьего порядка на .

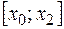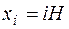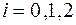8. Даны значения функции в точках ( ). На 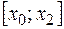существует ограниченная производная функции второго порядка 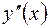. Для вычисления приближенного значения первой производной функции в точке 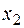используется формула:

.

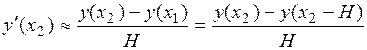Найти асимптотическую оценку погрешности этого приближенного значения.

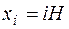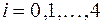9. Даны значения функции в точках ( ). На 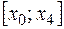существует ограниченная производная функции третьего порядка 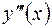. Для вычисления приближенного значения первой производной функции в точке 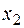используется формула:

.

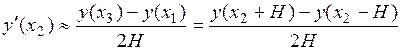Найти асимптотическую оценку погрешности этого приближенного значения.

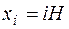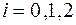10. Даны значения функции в точках ( ). На 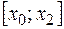существует ограниченная производная функции второго порядка 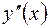. Для вычисления приближенного значения первой производной функции в точке 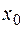используется формула:

.

Вычисление по этой формуле производятся на разреженной сетке с шагом :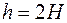

.

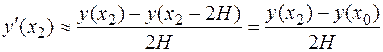Используя вторую формулу Рунге, уточнить полученное приближенное значение производной.

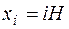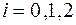11. Даны значения функции в точках ( ). На 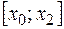существует ограниченная производная функции второго порядка 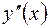. Для вычисления приближенного значения первой производной функции в точке 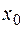используется формула:

.

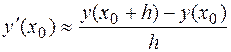Вычисление по этой формуле производятся на разреженной сетке с шагом :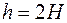

.

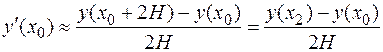Используя вторую формулу Рунге уточнить полученное приближенное значение производной.