Тема 4. Численное интегрирование.

1. Подобрать шаг интегрирования h и число отрезков разбиения n такие, чтобы приближенное значение интеграла , вычисляемое по обобщенной формуле средних прямоугольников, имело погрешность, не превышающую .

а) ; б) ; в) .

2. Подобрать шаг интегрирования h и число отрезков разбиения n такие, чтобы приближенное значение интеграла , вычисляемое по обобщенной формуле левых прямоугольников, имело погрешность, не превышающую .

а) ; б) ; в) .

3. Подобрать шаг интегрирования h и число отрезков разбиения n такие, чтобы приближенное значение интеграла , вычисляемое по обобщенной формуле трапеций, имело погрешность, не превышающую .

а) ; б) ; в) .

4. Подобрать шаг интегрирования h и число отрезков разбиения 2m такие, чтобы приближенное значение интеграла , вычисляемое по обобщенной формуле Симпсона, имело погрешность, не превышающую .

а) ; б) ; в) .

5. Подобрать шаг интегрирования h и число отрезков разбиения n такие, чтобы приближенное значение интеграла 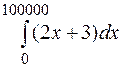, вычисляемое по обобщенной формуле трапеций, имело погрешность, не превышающую .

6. Подобрать шаг интегрирования h и число отрезков разбиения 2m такие, чтобы приближенное значение интеграла , вычисляемое по обобщенной формуле Симпсона, имело погрешность, не превышающую .

7. Записать формулу Гаусса с 3-мя узлами для вычисления интеграла и найти оценку абсолютной погрешности вычисленного по этой формуле приближенного значения интеграла для случая, когда , , .

8. Записать формулу Гаусса с 4 узлами для вычисления интеграла и найти оценку абсолютной погрешности вычисленного по этой формуле приближенного значения интеграла для случая, когда , , .

9. Подготовить все необходимое для вычисления приближеного значения несобственного интеграла I с погрешностью, не превышающей .

а) ; б) .

10. Подготовить все необходимое для вычисления приближенного значения несобственного интеграла I с погрешностью, не превышающей .

а) ; б) .