
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 1. Многочленная, кусочно-многочленная, сплайновая и обратная интерполяция.
1. Дана таблица значений некоторой функции  :
:
| x | -1 | |||
| y |
Построить по ней интерполяционный многочлен 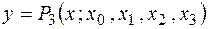 в форме Лагранжа.
в форме Лагранжа.
2. Дана таблица значений некоторой функции  :
:
| x | -1 | |||
| y |
Построить по ней интерполяционный многочлен 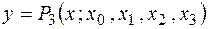 в форме Лагранжа.
в форме Лагранжа.
3. Дана таблица значений некоторой функции  :
:
| x | -1 | |||
| y |
Построить по ней интерполяционный многочлен 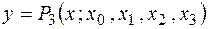 в форме Ньютона.
в форме Ньютона.
4. Дана таблица значений некоторой функции  :
:
| x | -1 | |||
| y |
Построить по ней интерполяционный многочлен 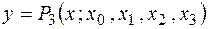 в форме Лагранжа.
в форме Лагранжа.
5. Дана таблица значений некоторой функции  :
:
| x | -1 | |||
| y |
Провести обратную интерполяцию, то есть построить
интерполяционный многочлен Ньютона  .
.
6.Дана таблица значений некоторой функции  :
:
| x | -1 | |||
| y |
Провести обратную интерполяцию, то есть построить интерполяционный многочлен Ньютона  .
.
7. Дана функция  .
.  ,
, 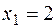 ,
,  . Приближение для функции строится в виде некоторого интерполяционного многочлена Лагранжа
. Приближение для функции строится в виде некоторого интерполяционного многочлена Лагранжа  . Найти оценку погрешности этого приближения как функцию х.
. Найти оценку погрешности этого приближения как функцию х.
8.  ,
, 
Записать интерполяционный многочлен Лагранжа десятого порядка  построенный по таблице значений этой функции, в виде:
построенный по таблице значений этой функции, в виде:  .
.
9. Дана таблица значений некоторой функции  и её производной:
и её производной:
| x | -1 | ||
| y | |||
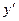
|
Построить по ней интерполяционный многочлен Эрмита 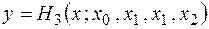 .
.
10.Дана таблица значений некоторой функции  и её производных:
и её производных:
| x | -1 | ||
| y | |||
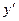
| |||
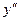
|
Построить по ней интерполяционный многочлен Эрмита.
11. Дана функция  ,
,  ,
, 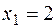 ,
,  . Приближение для функции строится в виде некоторого интерполяционного многочлена Лагранжа или Эрмита. Найти оценку погрешности этого приближения на
. Приближение для функции строится в виде некоторого интерполяционного многочлена Лагранжа или Эрмита. Найти оценку погрешности этого приближения на 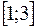 .
.
а) функция приближается многочленом Лагранжа 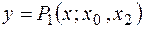 ;
;
б) функция приближается многочленом Лагранжа  ;
;
в) функция приближается многочленом Эрмита  ;
;
г) функция приближается многочленом Эрмита  .
.
Дата добавления: 2014-11-13; просмотров: 347; Мы поможем в написании вашей работы!; Нарушение авторских прав |