Зависимость между моментами силы относительно центра и относительно оси.

Пусть на тело действует приложен­ная в точке А сила F (рис. 33). Проведем какую - нибудь ось z и возьмем на ней произвольную точку О. Момент силы F относи­тельно центра О будет изображаться вектором М₀ перпендикуляр­ным плоскости ОАВ, причем по мо­дулю

.

Проведем теперь через любую точку O₁ на оси z плоскость ху, перпендику­лярную к оси; проектируя силу F на эту плоскость, найдем

.

Но треугольник О₁А₁В₁ представляет собою проекцию треуголь­ника ОАВ на плоскость ху. Угол между плоскостями этих треуголь­ников равен углу Рис. 33.

между перпендикулярами к плоскостям, т. е. ра­вен γ. Тогда, по известной геометрической формуле, .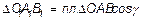

Умножая обе части этого равенства на 2 и замечая, что удвоен­ные пощади треугольников О₁А₁В₁ и ОАВ равны соответственно m_z(F) и М_о, найдем окончательно:

.

Так как произведение дает проекцию вектора на ось z, то равенство можно еще представить в виде

или .

В результате мы доказали, что между моментом силы относи­тельно оси и ее моментом относительно какого-нибудь центра, лежа­щего на этой оси, существует следующая зависимость: момент силы F относительно оси равен проекции на эту ось вектора, изображающего момент данной силы относительно любого центра, лежащего на оси.