Центры тяжести некоторых одно­родных тел.

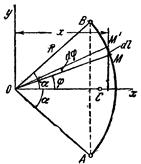1) Центр тяжести дуги окруж­ности. Рассмотрим дугу АВ радиуса R с центральным углом АОВ=2α. В силу сим­метрии центр тяжести этой дуги лежит на оси Ox (рис. 37). Найдем координату x_C по формуле 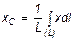. Для этого выделим на дуге АВ элемент ММ’ длиною dl = Rdφ, положение которого определяется углом φ. Координата х элемента ММ’ будет x = Rcosφ. Подставляя эти значения х и dl и имея в виду, что интеграл должен быть распространен на всю длину дуги, получим: Рис. 37.

где L - длина дуги АВ, равная R·2α. Отсюда окончательно нахо­дим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра О, равном

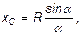
где угол α измеряется в радианах.

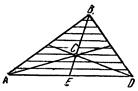2) Центр тяжести площади тре­угольника. Разобьем площадь треуголь­ника ABD (рис. 38) прямыми, параллель­ными AD, на п

узких полосок; центры тяжести этих полосок будут лежать на медиане BE треугольника. Следовательно, и центр тяжести всего тре­угольника лежит на этой медиане. Аналогичный результат получается для двух других медиан. Отсюда заключаем, что центр тяжести площади

треугольника лежит в точке пересечения его медиан.

При этом, как известно, Рис. 38.

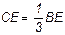
3) Центр тяжести площади кругового сектора. Рассмотрим круговой сектор ОАВ радиуса R с центральным углом 2α (рис. 39). Разобьем мысленно площадь сектора ОАВ радиусами, проведенными из центра О, на п секторов. В пределе, при неограниченном увеличении числа п, эти секторы можно рассматривать как плоские треугольники, центры тяжести которых лежат на дуге DE радиуса 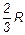. Следовательно, центр тяжести сектора ОAB будет со­впадать с центром тяжести дуги DE. Окончательно получим, что центр тяжести площади кругового сектора лежит на его центральной оси

симметрии на расстоянии от начального центра О, равном

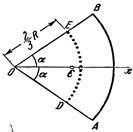
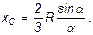
Рис. 39

Рекомендуемая литература.

1. Яблонский А.А. Курс теоретической механики. Т. 1,2. - М.: Высш. шк., 1977.

2. Добронравов В.В., Никитин Н.Н. Курс теоретической механики. - М.,1980.

3. Тарг С.М. Краткий курс теоретической механики. - М.: Высш. шк., 1986.

4. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики. Т.1,2. - М., 1982.