
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Приведение пространственной системы сил к данному центру.










 Полученные выше результаты позволяют решить задачу о приведении любой системы сил к данному центру. Эта задача, решается с помощью теоремы о параллельном переносе силы. Для переноса действующей на абсолютно твердое тело силы F из точки А (рис. 34, а) в точку О прикладываем в точке О силы F’ = F и F" = -F. Тогда сила F’ = F окажется приложенной в точке О и к ней будет присоединена пара (F, F") с моментом т, что Рис. 34.
Полученные выше результаты позволяют решить задачу о приведении любой системы сил к данному центру. Эта задача, решается с помощью теоремы о параллельном переносе силы. Для переноса действующей на абсолютно твердое тело силы F из точки А (рис. 34, а) в точку О прикладываем в точке О силы F’ = F и F" = -F. Тогда сила F’ = F окажется приложенной в точке О и к ней будет присоединена пара (F, F") с моментом т, что Рис. 34.
можно показать еще так, как на рис. 34, б. При этом
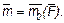


 Рассмотрим теперь твердое тело, на которое действует какая угодно система сил F1, F2, …, Fn (рис. 35, а). Выберем произвольную точку О за центр приведения и перенесем все силы системы в этот центр, присоединяя при этом соответствующие пары. Тогда на тело будет действовать система сил
Рассмотрим теперь твердое тело, на которое действует какая угодно система сил F1, F2, …, Fn (рис. 35, а). Выберем произвольную точку О за центр приведения и перенесем все силы системы в этот центр, присоединяя при этом соответствующие пары. Тогда на тело будет действовать система сил





 F’1 = F1, F’2 = F2, …, F’n = Fn.
F’1 = F1, F’2 = F2, …, F’n = Fn.
приложенных в центре О, и система пар, моменты которых будут равны








 m1 = m0(F1), m2 = m0(F2), …, mn = m0(Fn),
m1 = m0(F1), m2 = m0(F2), …, mn = m0(Fn),
 Силы, приложенные в точке О, заменяются одной силой R, приложенной в той же точке. При этом
Силы, приложенные в точке О, заменяются одной силой R, приложенной в той же точке. При этом  или,
или,
 .
.
Чтобы сложить все полученные пары, надо геометрически сложить векторы моментов этих пар. В результате система пар заменится одной парой, момент которой  или,
или,
 .
.

 Как и в случае плоской системы, величинаR, равная геометрической сумме всех сил, называется главным вектором системы; величина Мо, равная геометрической сумме моментов всех сил относительно центра О, называется главным моментом системы относительно этого центра.
Как и в случае плоской системы, величинаR, равная геометрической сумме всех сил, называется главным вектором системы; величина Мо, равная геометрической сумме моментов всех сил относительно центра О, называется главным моментом системы относительно этого центра.




 Таким образом мы доказали следующую теорему, любая система сил, действующих на абсолютно твердое тело, при приведении к произвольно взятому центру О заменяется одной силойR, равной главному вектору системы и приложенной в центре приведения О, и одной парой с моментом Мо, равным главному моменту системы относительно центра О (рис. 35, б).
Таким образом мы доказали следующую теорему, любая система сил, действующих на абсолютно твердое тело, при приведении к произвольно взятому центру О заменяется одной силойR, равной главному вектору системы и приложенной в центре приведения О, и одной парой с моментом Мо, равным главному моменту системы относительно центра О (рис. 35, б).
Векторы R и Mо обычно определяют аналитически, т. е. по их проекциям
на оси координат. Рис. 35.
Выражения для Rx, Ry, Rz нам известны.
 Проекции вектора Мо на оси координат будем обозначать Mx, My, Mz. По теореме о проекциях суммы векторов на ось будет
Проекции вектора Мо на оси координат будем обозначать Mx, My, Mz. По теореме о проекциях суммы векторов на ось будет  или,
или,  . Аналогично находятся величины My и Mz.
. Аналогично находятся величины My и Mz.

 Окончательно для определения проекций главного вектора R и главного момента Мо получаем формулы:
Окончательно для определения проекций главного вектора R и главного момента Мо получаем формулы:
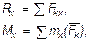


Дата добавления: 2014-12-23; просмотров: 421; Мы поможем в написании вашей работы!; Нарушение авторских прав |