
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Среднее квадратическое отклонение и коэффициент вариации определяются по формулам (5) и (6).
_____
s = Ös2 .
 |
При решении задачи 3.2 необходимо изучить тему "Выборочное наблюдение", разобраться в понятиях генеральной и выборочной совокупности и их характеристиках [1, с.101-107, 121-123;2, с.161-163;3, с.40-41]. Доверительные интервалы для генеральной средней определяются по формуле (7).
 |
где Dx – предельная ошибка выборочной средней, определяемая по формуле (8) для бесповторного отбора, t – коэффициент доверия к результатам, зависящий от вероятности.
Наиболее часто используются следующие значения вероятности и коэффициентов доверия:
при Р = 0,683; t = 1
Р = 0,954; t = 2
Р = 0,997; t = 3
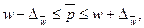 |
Доверительные интервалы для генеральной доли определяются по формуле (9).
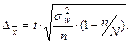 |
где Dw – предельная ошибка выборочной доли, определяемая по формуле (10).
Выборочная доля w = m/n, где m – количество единиц в выборке, имеющих признак, n – общее количество единиц в выборке. Дисперсия доли определяется по формуле s2w = w×(1- w). Отношение n/N называется долей выборки, т.е. какую часть составляет выборка в генеральной совокупности.
Пример 3. Имеются данные выборочного собственно-случайного бесповторного обследования 30% работников коммерческого банка об их стаже работы. Результаты обследования представлены в таблице 5.
Таблица 5
| Стаж работы, лет | До 3 | 3-5 | 5-7 | 7-9 | Свыше 9 | Итого |
| Число работников, чел. |
Дата добавления: 2014-12-23; просмотров: 322; Мы поможем в написании вашей работы!; Нарушение авторских прав |