
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Система нормальных уравнений для квадратичной модели (14) упрощается и позволяет рассчитать параметры модели путем решения системы двух уравнений с двумя неизвестными.
 |
Подробно расчет параметров линейной и других моделей тренда представлен в [1, с. 202-205].
Пример 4. Имеются данные о потреблении овощей на одного члена семьи по району за 1991 –1999 г. (таблица 9).
Таблица 9
| Год | |||||||
| У(t) | 10.0 | 10.5 | 12.0 | 10.2 | 13.0 | 16.3 | 18.0 |
Построить модель тренда методом аналитического выравнивания по прямой.
Решение: Для определения параметров модели построим расчетную таблицу 10.
Таблица 10
| Год | Потребление овощей, кг. yi | t | t2 | yi*t | yt = 12,86+ +1,3*t |
| 10,0 | -3 | -30,0 | 8,96 | ||
| 10,5 | -2 | -21,0 | 10,26 | ||
| 12,0 | -1 | -12,0 | 11,56 | ||
| 10,2 | 12,86 | ||||
| 13,0 | 13,0 | 14,16 | |||
| 16,3 | 32,6 | 15,46 | |||
| 18,0 | 16,76 | ||||
| Итого | 36,6 | 90,02 |
 |
По данным расчетной таблицы 10 определим параметры линейной модели тренда yt = a0 +a1 *t.
Рассчитаем значения yt по построенной модели yt = 12,86 + 1,3*t. Расчетные данные приведены в последней колонке таблицы 10. Для наглядного представления основной тенденции развития явления строится график фактических данных и модели тренда.
При решении задачи 6 необходимо изучить тему "Статистический анализ сезонных колебаний в ряде динамики" [1, с. 206-211;2,с.241-243;3, с. 58-62]. Уровень сезонности оценивается с помощью индексов сезонности. Если в ряду динамики отсутствует тренд или он незначителен, то для каждого месяца (квартала) индексы сезонности определяются по формуле
 |
__ __
где - yi – средняя за одноименные месяца (квартала), y – общая средняя за все года и месяца.
Решение задачи 6 представляется в виде таблицы расчета индексов сезонности и графически в виде сезонной волны. По оси ОХ откладываются месяцы (квартала), по оси ОУ – индексы сезонности.
Задача 7. Представлена на тему"Индексы".Для решения задачи необходимо изучить тему "Индексы". Расчет агрегатных индексов подробно разобран в [1, с. 227-231,241-244;2, с. 292-296;3, с. 69-71, 72-75], средних из индивидуальных индексов в [1, с. 230, 257;2, с. 301-303;3, с. 71, 74-76], индексов переменного состава, фиксированного состава и индекса структурных сдвигов в [1, c. 235-237, 250-252;2, с.304-306;3, с. 79-80].
Агрегатные индексы можно рассчитать по следующим формулам:
 |  |
- Индексы цен и физического объёма продукции
 |
_- Индекс стоимости продукции (товарооборота)
 |  |
- Индексы себестоимости и физического объёма
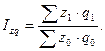 |
- Индекс затрат на производство
Между этими индексами имеется взаимосвязь Ip*Iq = Ipq и
Iz*Iq = Izq.
Индекс товарооборота характеризует относительное изменение (в %), а разность числителя и знаменателя индекса – абсолютное изменение (в руб.) фактической стоимости продукции в отчетном периоде по сравнению с базисным периодом. Индекс цен характеризует относительное изменение (в %), а разность числителя и знаменателя – абсолютное изменение (в руб.) стоимости продукции в отчетном периоде по сравнению с базисным периодом под влиянием изменения цен. Индекс физического объёма продукции характеризует относительное изменение (в %), а разность числителя и знаменателя – абсолютное изменение (в руб.) стоимости продукции в отчетном периоде по сравнению с базисным периодом под влиянием изменения объёмов производства (реализации) продукции.
Индексы переменного состава, фиксированного состава и индекс структурных сдвигов применяются при изучении динамики среднего качественного показателя (цены, себестоимости, выработки и т.д.) по одному виду продукции, производимому или реализуемому в различных местах. На динамику среднего качественного показателя оказывают влияние изменение самого этого показателя в каждом месте и структура (удельный вес каждого места в общем объёме производства или реализации продукции).
 |
Индекс переменного состава имеет вид:
где x – индексируемая величина (качественный показатель – себестоимость, выработка и т.д.);
d – структура, определяемая по формуле – di = qi /S qi или di = Ti /S Ti. Структура рассчитывается всегда по количественному показателю.
 |  |
Индекс фиксированного состава и индекс структурных сдвигов имеют вид:
Индекс переменного состава показывает, как изменяется в среднем индексируемая величина в отчетном периоде по сравнению с базисным периодом под влиянием двух факторов – изменения самой индексируемой величины и изменения структуры. Индекс фиксированного состава характеризует среднее изменение индексируемой величины под влиянием только первого фактора, а индекс структурных сдвигов – под влиянием второго фактора.
Дата добавления: 2014-12-23; просмотров: 325; Мы поможем в написании вашей работы!; Нарушение авторских прав |